Table of contents
- What Is Multiple Linear Regression (MLR)?
- What Are The Applications?
- When to Use the Multiple Regression Line Model?
- The Multiple Linear Regression Equation
- What is the Adjusted R Squared Ratio?
- What is the Predicted R-squared?
- Multiple Linear Regression on Excel
- Online Multiple Regression Calculators
- Related Articles
Estimated reading time: 8 minutes
What Is Multiple Linear Regression (MLR)?
Multiple Linear Regression (MLR) is a statistical method used to analyze the relationship between a dependent variable and two or more independent variables. It extends the concept of simple linear regression, which involves predicting a dependent variable based on a single independent variable, to cases where there are multiple predictors. It serves to predict the change in the dependent variable based on the difference in the independent variable; this could also be called a Multiple regression line. In this blog, you’ll also learn how to create multiple linear regression with r on Excel as well as 3 multiple regrregression equation calculator webpages that will help you create them quickly.
What Are The Applications?
Multiple Regression helps in a wide range of fields. Human Resource professionals might collect data about an employee’s salary based on factors such as work experience and competence. Your data can be used to build a model and determine employee wages. Is it more for certain groups of employees than the norm? Are there any employees or groups that are paid less than the norm?
Similar to the above, different researchers may use regression to determine which variables can best predict a specific outcome. To best match the results, deciding what independent variables are required is necessary. Which factors determine how schools score on their tests? What factors affect the productivity of a supply chain?
When to Use the Multiple Regression Line Model?
Simple linear regression serves as a tool enabling analysts or statisticians to forecast one variable’s behavior by leveraging known information about another variable. Its applicability arises in scenarios with two continuous variables—a dependent and an independent variable. The independent variable acts as the factor employed in determining the dependent variable or resultant outcome. When considering multiple regression, the model expands to encompass numerous explanatory variables, broadening its predictive capacity beyond singular factors.
The Multiple Linear Regression Equation
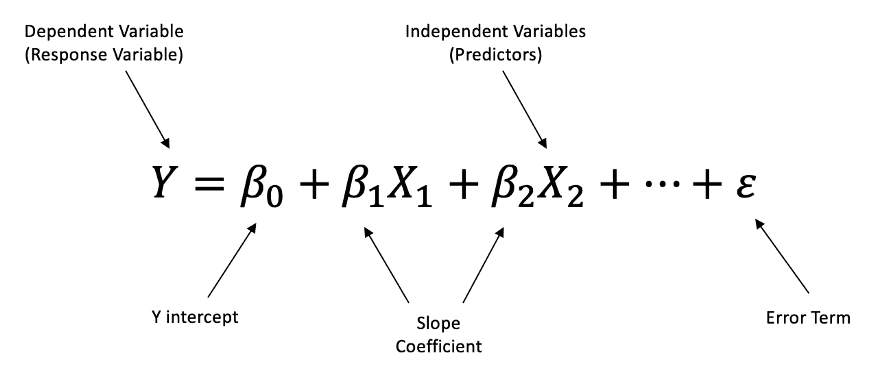
Y=β0+β1X1+β2X2+…+βnXn+ε
Where:
- Y is the dependent variable being predicted.
- 0β0 is the intercept or constant term.
- 1,2,…β1,β2,…βn are the coefficients associated with each independent variable 1,2,…X1, X2,…Xn respectively, representing their impact on Y.
- ε is the error term accounting for the difference between the predicted and actual values of Y.
This multiple linear regression equation signifies that the dependent variable Y is a linear combination of the independent variables 1,2,..X1, X2,…Xn weighted by their respective coefficients 1,2,…β1,β2,…βn, along with an intercept term 0β0. The goal of multiple linear regression is to estimate the coefficients that minimize the overall difference between predicted and actual values of the dependent variable.
What is the Adjusted R Squared Ratio?
The adjusted R squared measures the explanatory power for regression models with different numbers of predictors.
Let’s say you want to compare a five-predictor prediction model with a higher R squared to a one-predictor model. Is the R-squared higher for the five-predictor models because they are better? Is the R squared higher simply because there are more predictors? To find out, simply compare the adjusted R-squared values!
The adjusted R squared is a modified R squared, which has been adjusted to account for the number of predictors in a model. The adjusted R squared will increase if the new term makes the model better than expected. It drops if a predictor makes the model more accurate than it would be by chance. Although the adjusted R-squared may be harmful, it is usually not. It is always lower than the R squared.
Below is a simplified output of Best Subsets Regression. You can see the peaks and declines in the adjusted R squared. Nevertheless, R squared is increasing.
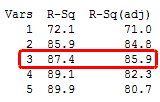
This model might only include three predictors. We saw in my previous blog how a poorly-specified model can lead to biased estimates. An oversimplified model (one with too many variables) will result in lower precision estimates and predictions. Therefore, don’t include terms that are not necessary in your model.
What is the Predicted R-squared?
The predicted R squared measures how accurately a regression model predicts new observations. This statistic can be used to determine if the model is able to predict new observations, but not the original data.
Mini-tab calculates predicted R squared by subtracting each observation from the data, then estimating the regression equation and determining how well it predicts the missing observation. Predicted R-squared is similar to adjusted R-squared and can be negative. It is always lower than R squared.
Even if the model isn’t used for predictions, the R-squared predicted still offers crucial information. It has the key advantage of preventing you from overfitting models. Overfitting a model with too many predictors can lead to it modeling random noise.
It’s impossible to predict random noise so the R-squared for an overfit model must decrease. A predicted R squared lower than the regular R squared is almost always a sign that there are too many terms in your model.
Multiple Linear Regression on Excel
This tutorial from Statology explains how to perform multiple linear regression in Excel.
Note: If you only have one explanatory variable, you should instead perform simple linear regression on Excel.
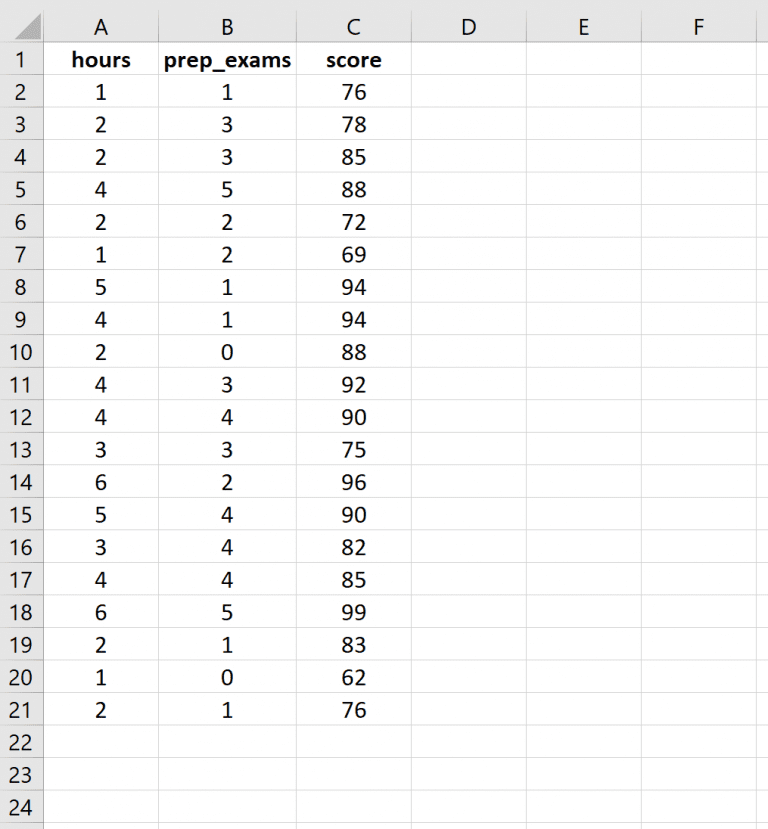
Step 1: Enter the data.
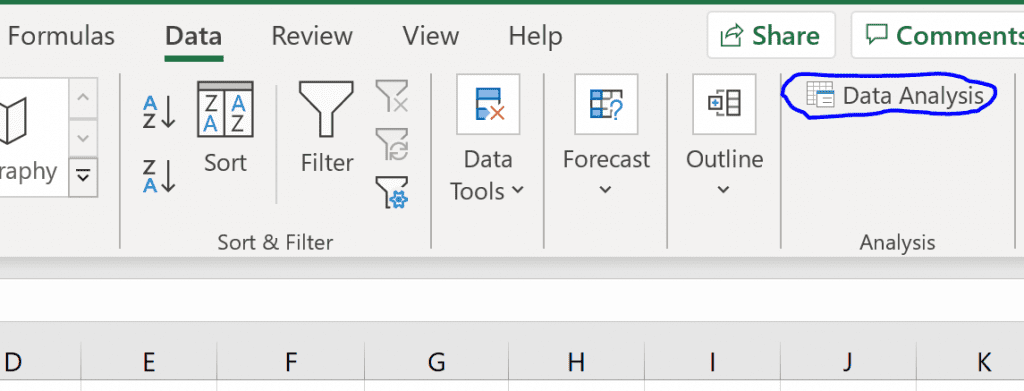
Step 2: Perform multiple linear regression.
Along with the top ribbon in Excel, go to the Data tab and click on Data Analysis. If you don’t see this option, then you need to first install the free Analysis ToolPak.
Once you click on Data Analysis, a new window will pop up. Select Regression and click OK.
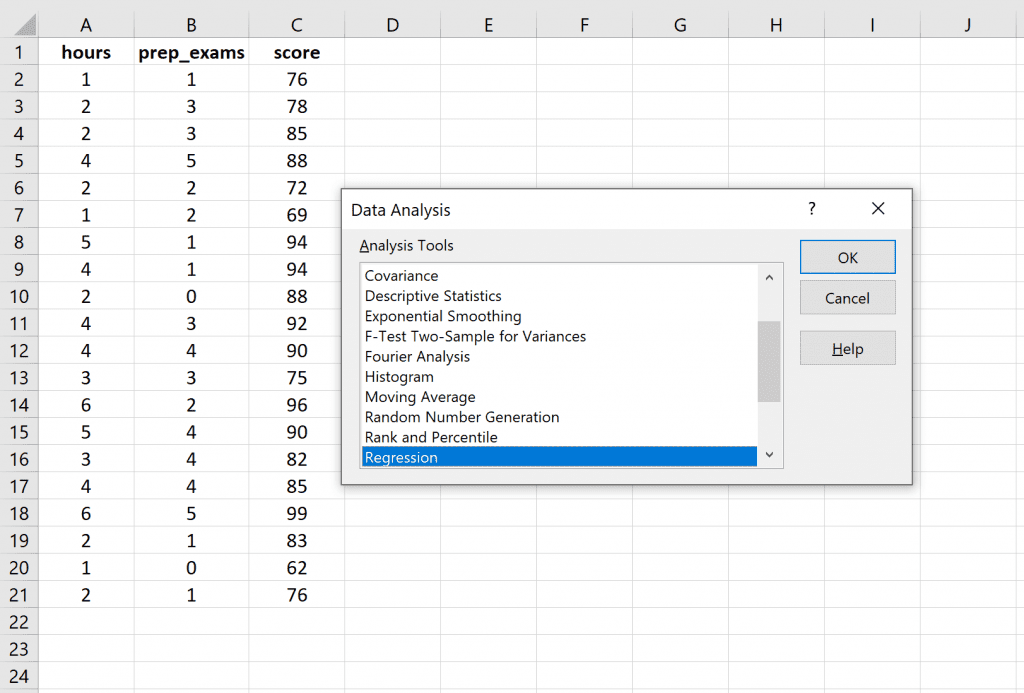
For the Input Y Range, fill in the array of values for the response variable. For Input X Range, fill in the array of values for the two explanatory variables. Check the box next to Labels so Excel knows that we included the variable names in the input ranges. For Output Range, select a cell where you would like the output of the regression to appear. Then click OK.
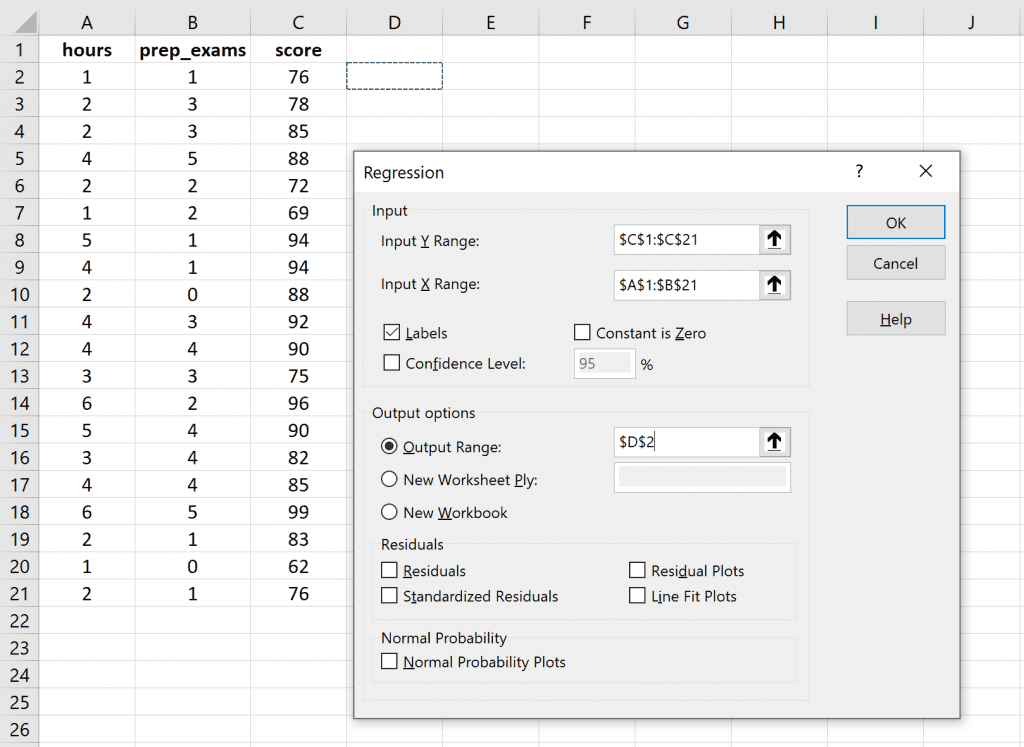
The following output will automatically appear:
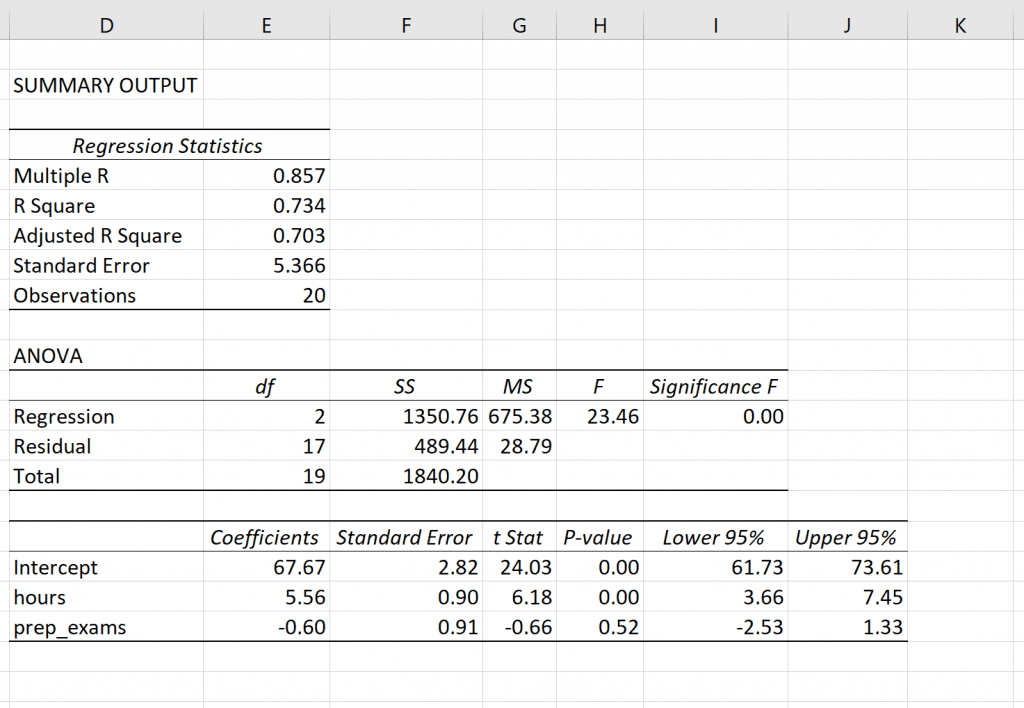
Step 3: Interpret the output.
Online Multiple Regression Calculators

This simple multiple regression line calculator uses the least-squares method to find the line of best fit for data comprising two independent X values and one dependent Y value, allowing you to estimate the value of a dependent variable (Y) from two given independent (or explanatory) variables (X1 and X2).
This multiple regression calculator makes use of variable transformations and calculates R, the Linear equation, and the p-value. It also calculates outliers and the adjusted Fisher-Pearson coefficient for skewness. The program interprets the results after confirming the residuals’ normality and multicollinearity. It then draws a histogram and residuals QQ plots, a correlation matrix, and a distribution graph. You can transform the variables, exclude any predictor, or run backward stepwise and select automatically based on the predictor’s predicted p-value.
Stats Solver:
Stats Solver is a multiple regression equation calculator that aims to solve any statistical problem quickly and easily. Use our intuitive interface to enter your problem and receive a step-by-step solution. Even if you don’t have an issue to solve, there are still ways you can learn from other examples. This multiple regression calculator will allow you to see if the solution changes, and you can change values quickly. To find out more about the topic, click on definitions, formulas, and explanations at the bottom of each page.



















