Table of contents
When the “P” is Low, the “Ho” Must Go!
Most people who run one sample t-test in a statistical package like Minitab trust the P-Value to inform them whether to trust the Null Hypothesis.
Just because the “P is Low,” it doesn’t always mean that “the Ho Must Go.” Understanding the issues and inputs related to the One Sample T-test will give you a more reliable determination.
Below is an example of a One Sample T Test and the most common issue that is challenged:
Example One Sample T Test
A supplier of a part to a large organization claims that the average(mean) weight of a part is 90 grams. The organization took a small sample of 20 parts and found that the mean score is 84 grams and the standard deviation is 11. Could this sample originate from a population of mean = 90 grams?
- Hypothesised Mean = 90
- N Sample size (# of Parts) = 20
- X-Bar (Average of the Samples) = 84
- S (Standard Deviation) = 11
- Delta or Change = 6
The organization wants to test this at a significance level of 0.05 (95% Confidence), i.e. it is willing to take only a 5 percent risk of being wrong when it says the sample is not from the population. Therefore:
- Null Hypothesis (H0): “True Population Mean Score = 90”
- Alternative Hypothesis (Ha): “True Population Mean Score is not = 90”
- Alpha (Risk) is 0.05
Logically, the farther away the Observed or Measured Sample Mean is from the Hypothesized Mean, the lower the probability (i.e., the P-value) that the Null Hypothesis is true. However, what is far enough? In this example, the difference (Delta) between the Sample Mean and the Hypothesized Population Mean is 6. Is that difference big enough to reject H0 based on the test results and information provided?
First, the sample size needs to be large enough to detect the difference.
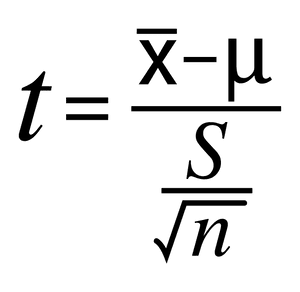
In this case, the required sample size to be able to detect a true difference between populations is 38 (use the One Sample T-test Power and sample size calculator in Minitab).
With a sample size of 20, if the difference is less than 8.4 the test is not definitive or sensitive enough to detect a true shift. If you use the supplied data in the summarized T-test you will get a low P value – which may be challenged and questioned by someone who is familiar with Hypothesis Testing.
Don’t worry too much about understanding the calculations because most statistical packages, like Minitab, will calculate Sample Sizes, T-Test Statistics, and P-Value for you.
If interested, you can compare the T-Value generated with the Critical Value of T. You can find the Critical T Value on the following website: https://people.richland.edu/james/lecture/m170/tbl-t.html. Cross-reference the Confidence Level with the ‘DF’ (Degrees of Freedom) to find the Critical T-value.
The Critical T-Value marks the threshold that, if it is exceeded, leads to the conclusion that the difference between the observed Sample Mean and the Hypothesized Population Mean is large enough to reject H0. The Critical T-Value equals the value whose probability of occurrence is less or equal to 5 percent. From the T-Distribution Tables, one can find that the Critical Value of T is +/- 2.093.
Since the retrieved T-Value of -2.44 is smaller than the Critical Value of -2.093, the Null Hypothesis must be rejected (i.e., the Sample Mean is not from the Hypothesized Population) and the supplier’s claims may be questioned. However, the base issue related to sample size needs to be addressed first.
Has the P-Value ever led you to the wrong conclusion? Was your sample size sufficient to make the correct determination?
Share your thoughts in the comments below!



















