
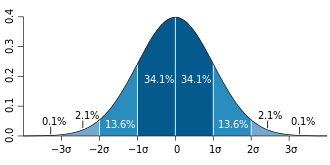
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low S.D. indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high S.D. indicates that the values are spread out over a wider range.
Standard deviation may be abbreviated SD, and is most commonly represented in mathematical texts and equations by the lower case Greek letter sigma σ, for the population standard deviation, or the Latin letter s, for the sample standard deviation.
The S.D. of a random variable, sample, statistical population, data set, or probability distribution is the square root of its variance. It is algebraically simpler, though in practice, less robust than the average absolute deviation. A useful property of this measure is that unlike the variance, it is expressed in the same unit as the data.
This measure of a population or sample and the standard error of a statistic (e.g., of the sample mean) are quite different, but related. The sample mean’s standard error is the standard deviation of the set of means that would be found by drawing an infinite number of repeated samples from the population and computing a mean for each sample. The mean’s standard error turns out to equal the population standard deviation divided by the square root of the sample size, and is estimated by using the sample standard deviation divided by the square root of the sample size. For example, a poll’s standard error (what is reported as the margin of error of the poll), is the expected S.D. of the estimated mean if the same poll were to be conducted multiple times. Thus, the standard error estimates the S.D. of an estimate, which itself measures how much the estimate depends on the particular sample that was taken from the population.
References
Wikipedia. https://en.wikipedia.org/wiki/Standard_deviation


















