A well-determined sample size ensures that the research conclusions are valid and applicable to the larger population from which the sample was drawn.
Table of contents
Definition of Sample Size
Sample size refers to the number of observations or data points included in a study. In research, the size of the sample is critical because it directly affects the accuracy, reliability, and generalizability of the study findings.
Why does the Size of the Sample Matters?
- Precision: A larger sample size increases the precision of the study’s estimates. Precision refers to the closeness of the sample estimates to the actual population parameters. Larger samples provide more data points, which help in achieving more accurate and reliable estimates.
- Power of the Study: The power of a study is its ability to detect a true effect or difference when it exists. A study with a small sample size may fail to detect significant differences or effects, leading to a Type II error (false negative). Conversely, an adequately powered study with an appropriate size of the sample reduces the risk of missing significant findings.
- Generalizability: A sample size that is representative of the population ensures that the study findings can be generalized to the entire population. If the sample is too small or biased, the results may not be applicable to the broader population.
- Confidence Levels and Intervals: The Size of the sample affects the confidence level and the width of the confidence intervals around the study estimates. Larger sample sizes lead to narrower confidence intervals, providing more precise estimates of the population parameters.
Factors Influencing Sample Size Determination
Determining the appropriate size of the sample involves considering several factors, including the research objectives, the design of the study, and the statistical methods used. Key factors include:
- Effect Size: The magnitude of the difference or relationship that the study aims to detect. Smaller effect sizes require larger sample sizes to achieve the same level of statistical power.
- Variability: The extent of variability or dispersion in the data. Higher variability in the population necessitates a larger sample size to accurately estimate the population parameters.
- Desired Confidence Level: The probability that the confidence interval contains the true population parameter. Commonly used confidence levels are 90%, 95%, and 99%. Higher confidence levels require larger sample sizes.
- Statistical Power: The probability of correctly rejecting the null hypothesis when it is false. A higher power (typically 0.80 or 80%) increases the likelihood of detecting a true effect and requires a larger sample size.
- Significance Level (Alpha): The probability of making a Type I error (false positive). Common significance levels are 0.05, 0.01, and 0.10. Lower significance levels require larger sample sizes.
Methods for Determining Size of the Sample

Several methods can be used to determine the appropriate size of the sample for a study:
- Formulas and Statistical Calculations: Various statistical formulas and tables can help calculate sample size based on the desired power, effect size, variability, confidence level, and significance level. These formulas differ based on the type of study (e.g., survey, experiment) and the nature of the data (e.g., continuous, categorical).
- Power Analysis: Power analysis involves calculating the size of the sample required to achieve a specified level of power for detecting a given effect size. This method is particularly useful in experimental and clinical research.
- Pilot Studies: Conducting a pilot study with a smaller sample can provide preliminary data on variability and effect size, which can be used to calculate the size of the sample for the main study.
- Software Tools: Various software tools and online calculators are available to assist researchers in determining the appropriate size of the sanple. These tools often require inputs such as effect size, variability, power, confidence level, and significance level.
Examples
Example 1: Clinical Trial
In a clinical trial comparing a new drug to a standard treatment, researchers aim to detect a 10% improvement in patient outcomes with 80% power and a 5% significance level. Based on preliminary data, the standard deviation of outcomes is estimated to be 15%.
Using a sample size formula for comparing two means:
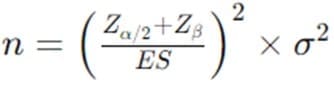
Where:

Plugging in the values, the required size of the sample per group is calculated.
Example 2: Survey Research
In a survey aiming to estimate the proportion of a population with a certain characteristic with 95% confidence and a margin of error of 5%, researchers need to determine the size of the sample.
Using the formula for estimating a proportion:
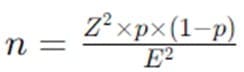
Where:
- ZZZ is the critical value for 95% confidence (1.96)
- ppp is the estimated proportion (0.5 for maximum variability)
- EEE is the margin of error (0.05)
Plugging in the values, the required sample size is calculated.
Challenges and Considerations
- Non-Response and Attrition: In survey research and longitudinal studies, non-response and attrition can reduce the effective size. Researchers should account for potential non-response by increasing the initial size of the sample.
- Resource Constraints: Budget, time, and logistical constraints may limit the feasible size of the sample. Researchers must balance the need for a large sample with the available resources.
- Ethical Considerations: In clinical research, ethical considerations may limit the size. particularly when dealing with vulnerable populations or invasive procedures.
- Population Characteristics: The characteristics of the population, such as its heterogeneity and accessibility, can impact sample size determination. Stratified sampling or oversampling specific subgroups may be necessary to ensure representativeness.
Final Words
Sample size determination is a critical aspect of research design that influences the validity, reliability, and generalizability of study findings. It requires careful consideration of factors such as effect size, variability, confidence level, statistical power, and significance level.
Researchers can use various methods, including statistical formulas, power analysis, pilot studies, and software tools, to calculate the appropriate size of the sample. By addressing potential challenges and considerations, researchers can ensure that their studies are robust and produce meaningful and accurate results.


















