In Null Hypothesis Significance Testing (NHST), statisticians use this fundamental method to determine whether they have enough evidence to reject a null hypothesis in favour of an alternative hypothesis. Researchers widely employ this method in scientific studies to infer conclusions about populations based on sample data.
The primary tool of NHST is the P value, a statistical measure that helps researchers determine the likelihood that the observed data would occur if the null hypothesis were true. Despite its widespread use, the P value is often misunderstood, and misinterpretation can lead to erroneous conclusions.
This post explores the concept of the null hypothesis, the role of the P value in NHST, and common misconceptions surrounding its use.
Table of contents
Null Hypothesis and Alternative Hypothesis
In NHST, the null hypothesis (H0) represents a statement of no effect, no difference, or no association between variables. It serves as a default position that assumes any observed differences or effects are due to chance rather than a true underlying effect. The alternative hypothesis (Ha), on the other hand, posits that there is a genuine effect, difference, or association.
For example, consider a clinical trial evaluating a new drug. If the current standard treatment is 25% effective, the null hypothesis might state that the new drug is no more effective than the standard treatment (H0: p = 0.25). The alternative hypothesis would propose that the new drug is more effective (Ha: p > 0.25).
The goal of NHST is to assess whether the observed data provides sufficient evidence to reject the null hypothesis in favour of the alternative hypothesis.
Historical and Philosophical Context
The concept of the null hypothesis has its roots in the works of early statisticians such as R.A. Fisher, who introduced it as a tool for hypothesis testing. Fisher’s approach emphasized using the P value as a rough guide to the strength of evidence against the null hypothesis. However, Fisher himself struggled to provide a clear inferential meaning for the P value.
The philosophical underpinnings of the null hypothesis are also influenced by thinkers like Francis Bacon and Karl Popper, who advocated for falsification and the use of negative instances to test scientific theories.
The null hypothesis aligns with these principles by providing a framework for testing whether observed patterns are due to random chance rather than a true underlying effect.
Key Terminology
Before delving deeper, let’s define some essential terms and acronyms related to NHST:
- P: Represents the P value, a critical statistic in hypothesis testing.
- p: Refers to the binomial parameter, denoting the probability of success in a binomial experiment.
- n: Represents the sample size, which is the number of observations or trials conducted.
- H0: Denotes the null hypothesis, which assumes no effect or difference.
- Ha: Denotes the alternative hypothesis, which asserts that there is an effect or difference.
Definition and Interpretation of P Value
The P value is a key component of NHST. It quantifies the probability of observing data as extreme as, or more extreme than, the observed data, assuming that the null hypothesis is true. Mathematically, the P value is defined as:
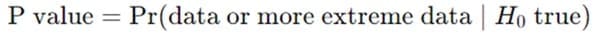
Here, denotes probability, and ∣\mid∣ signifies “given” or “conditional upon.” The P value answers the question: “If the null hypothesis were true, what is the probability of observing data as extreme as, or more extreme than, the data actually observed?”
Importantly, the P value does not indicate the probability that the null hypothesis is true or false. It assumes the null hypothesis is true and measures how well the observed data aligns with this assumption. A small P value suggests that the observed data is unlikely under the null hypothesis, providing evidence against it.
Classical Approaches to Interpreting the P-Value
There are two main classical approaches to interpreting the P value: the Fisherian approach and the Neyman-Pearson approach.
- Fisherian Approach: Proposed by Ronald A. Fisher, this approach uses the P value as a measure of evidence against the null hypothesis. Fisher suggested that a small P value indicates strong evidence against H0. Researchers using this approach may consider a P value less than 0.05 as evidence to reject the null hypothesis.
- Neyman-Pearson Approach: Developed by Jerzy Neyman and Egon Pearson, this approach emphasizes the use of pre-specified significance levels (alpha) and involves comparing the P value to this threshold. If the P value is less than the alpha level, the null hypothesis is rejected. This approach focuses on controlling the Type I error rate (the probability of rejecting a true null hypothesis).
Common Misconceptions about P Values
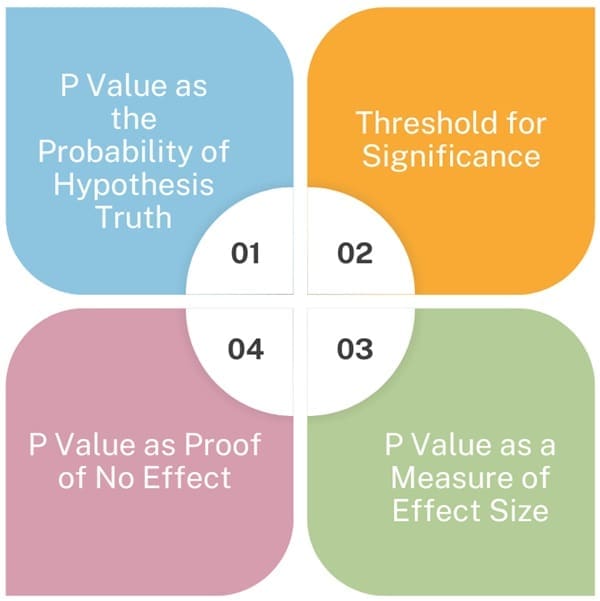
The interpretation of P values is fraught with misconceptions. Some common misunderstandings include:
- P Value as the Probability of Hypothesis Truth: A P value does not indicate the probability that the null hypothesis is true. It only measures the likelihood of observing the data if the null hypothesis is true.
- Threshold for Significance: The conventional threshold of 0.05 is often misinterpreted as an absolute cutoff. While P values less than 0.05 are typically considered significant, this threshold is arbitrary and context-dependent.
- P Value as a Measure of Effect Size: The P value does not provide information about the magnitude of an effect. It only indicates whether an effect is statistically significant.
- P Value as Proof of No Effect: A large P value does not prove that there is no effect; it only suggests that the data does not provide strong evidence against the null hypothesis.
Example of NHST
Consider a researcher testing the effectiveness of a new treatment. Suppose the existing treatment has a success rate of 25%. The null hypothesis is that the new treatment is not more effective than the existing one (H0: p = 0.25). The researcher tests the new treatment on 3 patients and observes the following outcomes:
- All 3 patients respond positively: P value = Pr (X=3) \ Pr(X = 3) Pr (X=3) = 0.0156.
- 2 out of 3 patients respond positively: P value = Pr (X=2) + Pr (X=3) \ Pr (X = 2) + \ Pr (X = 3) Pr (X=2) + Pr (X=3) = 0.1562.
In this scenario, a P value of 0.0156 suggests strong evidence against the null hypothesis, indicating that the new treatment might be more effective. However, a P value of 0.1562 suggests weak evidence against the null hypothesis, indicating that the observed result could be due to chance.
Conducting a Null Hypothesis Significance Test

The exact binomial test is a specific application of NHST for testing binomial proportions from a single sample. The procedure involves:
Step 1: Formulating Hypotheses
The first step in NHST is to clearly articulate the research question and formulate the null and alternative hypotheses.
- The null hypothesis (H0) typically states that there is no difference or effect. For instance, if a new treatment is believed to be 25% effective, the null hypothesis could be stated as: H0:p=0.25 H0: p = 0.25 H0:p=0.25
- The alternative hypothesis (Ha) posits that there is a difference or effect, expressed as Ha:p>0.25 Ha: p > 0.25 Ha:p>0.25
In this context, the parameter being studied is the proportion of successes in a sample, which follows a binomial distribution.
Step 2: Selecting the Statistical Model
After establishing the hypotheses, researchers select the appropriate statistical model to test them. They utilize the binomial probability mass function (pmf) for a binomial proportion. Under the null hypothesis, they model the number of successes in a given sample as:
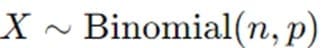
where n is the sample size, and p is the assumed success probability under H0.
Step 3: Calculating the P-Value
The next step involves calculating the P value based on the observed data. The P value reflects the probability of observing the data or something more extreme, given that the null hypothesis is true, and derives from the binomial distribution.
For example, if a researcher conducts a study with three patients and records the number of successful treatments, they would calculate the P value based on the observed number of successes.
- If all three patients respond positively to the treatment, the P value would be:
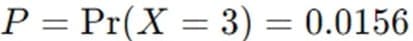
This indicates that such an outcome would be quite rare under the null hypothesis (H0: p = 0.25).
- Conversely, if only two out of three patients respond, the P value would be calculated as:
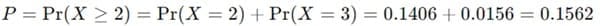
This suggests that the result is not statistically significant, as it does not provide strong evidence against the null hypothesis.
Step 4: Interpreting Results
The final step is to interpret the results of the hypothesis test. Researchers should report the sample proportion, the direction of the observed difference (if any), and the corresponding P value. A commonly accepted threshold for statistical significance is a P value less than 0.05.
However, exercise caution, as declaring a result “significant” merely based on this threshold can lead to misinterpretations.
Final Words
Null Hypothesis Significance Testing is a powerful tool for making inferences about populations based on sample data. The P value, as a measure of the probability of observing data under the null hypothesis, plays a central role in this process. However, the correct interpretation of P values requires an understanding of their limitations and the context in which they are used.
By recognizing common misconceptions and adhering to rigorous statistical practices, researchers can better utilize NHST to draw meaningful conclusions from their data.


















