Table of contents
Estimated reading time: 6 minutes
Response Surface Analysis: Complete Guide
Response Surface Analysis (RSA) is an indispensable statistical method that allows researchers and analysts to explore complex relationships between multiple variables and responses. This method, often implemented through response surface designs, is a powerful tool utilized across various fields to optimize processes, predict outcomes, and understand the interactions between factors affecting a response. Unraveling the intricacies of this method—the response surface method—provides a robust framework for enhancing efficiency and decision-making in experimental designs.
What is Response Surface Analysis?
At its core, Response Surface Analysis (RSA) is a statistical technique employed to study the relationship between multiple input variables and one or more responses. By using mathematical models to represent these relationships, RSA helps in optimizing and understanding the interaction effects among factors. Essentially, it explores the curvature of the response surface, enabling analysts to identify optimal conditions that yield the desired outcomes within the experimental space.
Basics of Response Surface Analysis (RSA)
Response Surface Analysis (RSA) is a powerful statistical and mathematical technique used to explore the relationships between multiple variables and their impact on one or more responses or outcomes. This method is particularly valuable in experimental design, helping researchers understand the complex interactions between factors and responses within a given system. RSA comprises several integral components, each playing a crucial role in constructing and interpreting the response surface design. These components include factors and levels, the design matrix, and response variables.
Components of RSA
Factors and Levels: Factors represent the variables under consideration, while levels denote the settings or values assumed by these factors during experimentation. Identifying appropriate factors and their corresponding levels is fundamental in building a comprehensive response surface model.
Design Matrix: A design matrix in RSA consists of planned combinations of factor levels. It dictates the layout of experiments necessary to gather data for constructing the response surface model. Diverse designs such as central composite designs or Box-Behnken designs are commonly employed to efficiently explore the factor space.
Response Variables: These are the outcomes or measures observed in response to changes in the factors. Response variables are pivotal in understanding how changes in the factors influence the desired outcomes, thereby aiding in optimizing the process.
Response Surface Analysis is a versatile and robust tool that enables researchers to navigate complex systems, optimize processes, and gain deeper insights into the relationships between variables and responses. Its application spans various fields, offering a systematic approach to experimental design and analysis.
Optimization Techniques in Response Surface Analysis
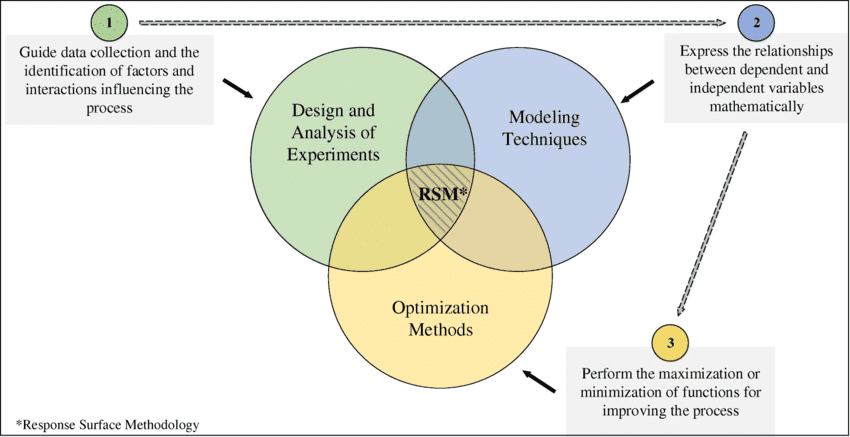
In the realm of response surface analysis, various optimization techniques and designs enhance the analysis process and aid in pinpointing optimal conditions for desired responses.
Desirability Function Approach: This approach allows analysts to optimize multiple responses simultaneously by assigning desirability values to each response. It helps in finding the best compromise among conflicting objectives.
Gradient-Based Optimization Methods: Utilizing gradients and derivatives, these methods explore the response surface to locate maximum or minimum points. Techniques like the steepest ascent or descent are commonly applied for optimization.
Monte Carlo Simulation: This stochastic technique involves running simulations based on random sampling from probability distributions of factors. It aids in understanding the variability and uncertainty within the response surface model.
Practical Applications of Response Surface Analysis
Practical applications of Response Surface Analysis (RSA) span across various industries and disciplines, owing to its versatile nature in optimizing processes, predicting outcomes, and understanding complex relationships among multiple variables. Some notable practical applications include:
Pharmaceutical Industry:
- Drug Formulation Optimization: RSA assists in optimizing drug formulations by examining factors like ingredient concentrations, pH levels, and temperature to enhance efficacy while minimizing side effects or production costs.
- Process Development: It aids in developing robust and efficient processes for pharmaceutical manufacturing, ensuring consistent quality and yield.
Manufacturing and Engineering:
- Process Optimization: RSA helps in optimizing manufacturing processes, such as chemical reactions, to achieve maximum yield while reducing waste and energy consumption.
- Product Design: In engineering, it aids in designing products by analyzing factors like material properties, dimensions, and environmental conditions to meet desired performance criteria.
Agriculture and Food Industry:
- Crop Yield Enhancement: In agriculture, RSA assists in optimizing factors like soil nutrients, irrigation, and crop management practices to maximize yield and quality.
- Food Product Development: It helps in developing new food products by optimizing ingredients, processing parameters, and packaging to meet consumer preferences and regulatory standards.
Environmental Science:
- Pollution Control: RSA is used to optimize environmental processes, such as wastewater treatment or air pollution control, by analyzing factors like temperature, pH, and chemical concentrations for effective mitigation.
Healthcare and Biotechnology:
- Bioprocess Optimization: RSA aids in optimizing bioprocesses for producing biofuels, enzymes, or biopharmaceuticals by studying factors affecting cell cultures or fermentation conditions.
- Clinical Trials: It assists in designing and optimizing clinical trials by identifying key factors impacting outcomes and refining experimental protocols.
Quality Control and Six Sigma Practices:
- Process Improvement: RSA is employed in quality control to identify factors causing variations in processes and to optimize them for consistent and high-quality output.
- Six Sigma Initiatives: It contributes to Six Sigma methodologies by aiding in process optimization and minimizing defects or deviations.
Chemical and Material Sciences:
- Material Development: RSA assists in developing new materials with optimized properties by studying factors like composition, temperature, and processing parameters.
- Chemical Reaction Optimization: It aids in optimizing chemical reactions for desired product yields, purity, or specific characteristics.
Marketing and Business:
- Market Research and Product Development: In business, RSA can be applied to optimize marketing strategies, pricing models, and product development by analyzing various factors affecting consumer preferences and market outcomes.
These practical applications of Response Surface Analysis highlight its widespread utility across diverse fields, emphasizing its role in optimizing processes, improving efficiency, and aiding decision-making in complex systems. Its ability to model and analyze multifaceted relationships among variables makes it an invaluable tool for researchers, engineers, analysts, and decision-makers across various industries.
How to Create a Response Surface Analysis
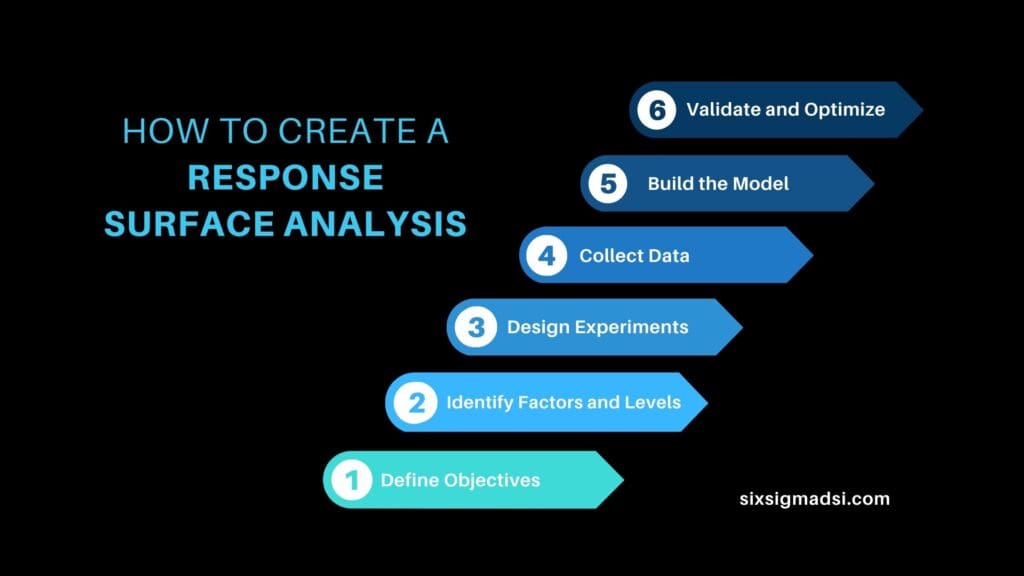
To embark on constructing a response surface analysis, follow these steps:
- Define Objectives: Clearly outline the goals and outcomes you aim to achieve through RSA.
- Identify Factors and Levels: Select relevant factors and determine the levels to be studied.
- Design Experiments: Employ suitable designs (central composite, Box-Behnken, etc.) to plan the experiments.
- Collect Data: Execute experiments and gather data on responses corresponding to different factor combinations.
- Build Model: Use statistical software to construct the response surface model based on collected data.
- Validate and Optimize: Validate the model and employ optimization techniques to find the optimal conditions.
Response Surface Analysis stands as a robust method offering a systematic approach to understanding complex relationships among multiple variables. This tool empowers industries and researchers to optimize processes, predict outcomes, and make informed decisions. Its versatility across domains and its capacity to unveil optimal conditions make it an invaluable asset in the arsenal of analytical tools.



















