In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, it is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane. In an experimental design, when the output of the process does not seem to vary linearly with the input factor in an experimental design, the output at the center point does not lie along a line between the output values at a low and at a high level of the input. Basically what you want to know is if there is a linear relationship between each X and Y or not, if you see curvature, it often indicates that your X settings are near an optimum Y, and you’ve discovered insightful results.
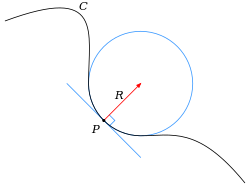
For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature at a point of a differentiable curve is the curvature of its osculating circle, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero, and of a curve at a point is normally a scalar quantity, that is, it is expressed by a single real number.
References
Wikipedia. https://en.wikipedia.org/wiki/Curvature


















