In statistics, Box–Behnken designs are experimental designs for response surface methodology, devised by George E. P. Box and Donald Behnken in 1960, to achieve the following goals:
- Each factor, or independent variable, is placed at one of three equally spaced values, usually coded as −1, 0, +1. (At least three levels are needed for the following goal.)
- The design should be sufficient to fit a quadratic model, that is, one containing squared terms, products of two factors, linear terms and an intercept.
- The ratio of the number of experimental points to the number of coefficients in the quadratic model should be reasonable (in fact, their design is kept in the range of 1.5 to 2.6).
- The estimation variance should more or less depend only on the distance from the center (this is achieved exactly for the designs with 4 and 7 factors), and should not vary too much inside the smallest (hyper)cube containing the experimental points. (See “rotatability” in “Comparisons of response surface designs“.)
The Box-Behnken design is an experimental design used in Response Surface Modeling to obtain polynomial equations with only three levels for each factor. It is still considered to be more proficient and most powerful than other designs such as the three-level full factorial design, central composite design (CCD) and Doehlert design, despite its poor coverage of the corner of nonlinear design space.
The Box-Behnken design with 7 factors was found first while looking for a design having the desired property concerning estimation variance, and then similar designs were found for other numbers of factors.
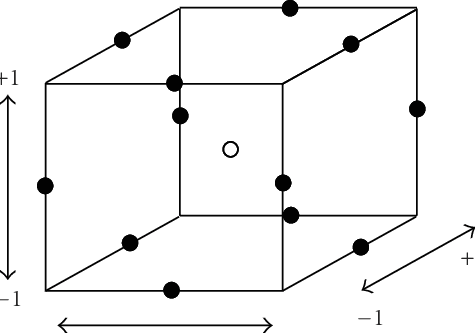
Each design can be thought of as a combination of a two-level (full or fractional) factorial design with an incomplete block design. In each block, a certain number of factors are put through all combinations for the factorial design, while the other factors are kept at the central values. For instance, the Box–Behnken design for 3 factors involves three blocks, in each of which 2 factors are varied through the 4 possible combinations of high and low. It is necessary to include center points as well (in which all factors are at their central values).
References
Wikipedia. Box-Behnken Design. https://en.wikipedia.org/wiki/Box%E2%80%93Behnken_design