In statistics, Bartlett’s test, named after Maurice Stevenson Bartlett, is used to test homoscedasticity, that is, if multiple samples are from populations with equal variances. Some statistical tests, such as the analysis of variance, assume that variances are equal across groups or samples, which can be verified with Bartlett’s test. In other words, it is a test for equal variances, assuming normal data.
In this test, we construct the null and alternative hypothesis. For this purpose, several test procedures have been devised. This test procedure is based on the statistic whose sampling distribution is approximately a Chi-Square distribution with (k-1) degrees of freedom, where k is the number of random samples, which may vary in size and are each drawn from independent normal distributions. This test is sensitive to departures from normality. That is, if the samples come from non-normal distributions, then Bartlett’s test may simply be testing for non-normality.
test is used to test the null hypothesis, H0 that all k population variances are equal against the alternative that at least two are different.
If there are k samples with sizes and sample variances then Bartlett’s test statistic is:
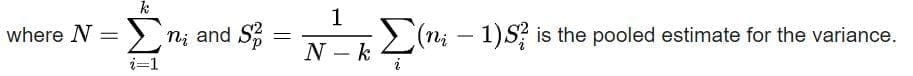
The test statistic has approximately a 
distribution. Thus the null hypothesis is rejected if
References
Wikipedia. https://en.wikipedia.org/wiki/Bartlett%27s_test
