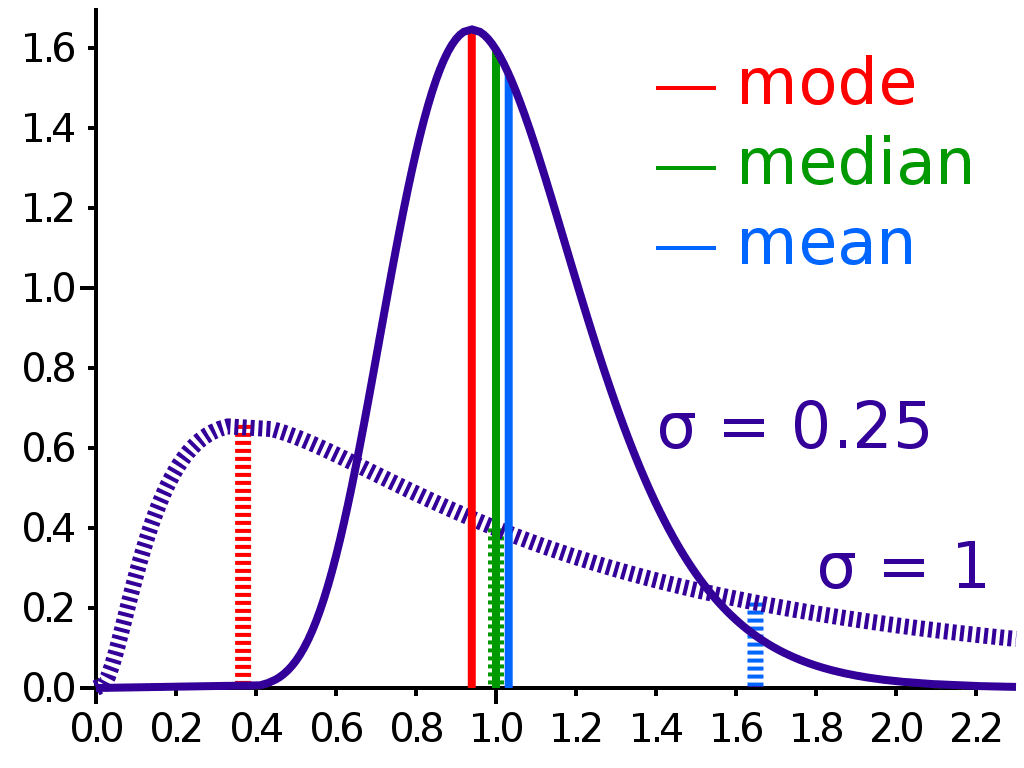
The mode is the value that appears most often in a set of data values. If X is a discrete random variable, it is the value x (i.e, X = x) at which the probability mass function takes its maximum value. In other words, it is the value that is most likely to be sampled.
Like the statistical mean and median, the mode is a way of expressing, in a (usually) single number, important information about a random variable or a population. The numerical value of this terms is the same as that of the mean and median in a normal distribution, and it may be very different in highly skewed distributions.
This term is not necessarily unique to a given discrete distribution, since the probability mass function may take the same maximum value at several points x1, x2, etc. The most extreme case occurs in uniform distributions, where all values occur equally frequently.
When the probability density function of a continuous distribution has multiple local maxima it is common to refer to all of the local maxima as modes of the distribution. Such a continuous distribution is called multimodal (as opposed to unimodal). A mode of a continuous probability distribution is often considered to be any value x at which its probability density function has a locally maximum value, so any peak is a mode.
References
Wikipedia. Mode (Statistics). https://en.wikipedia.org/wiki/Mode_(statistics)