Table of contents
What Is a Bimodal Histogram?
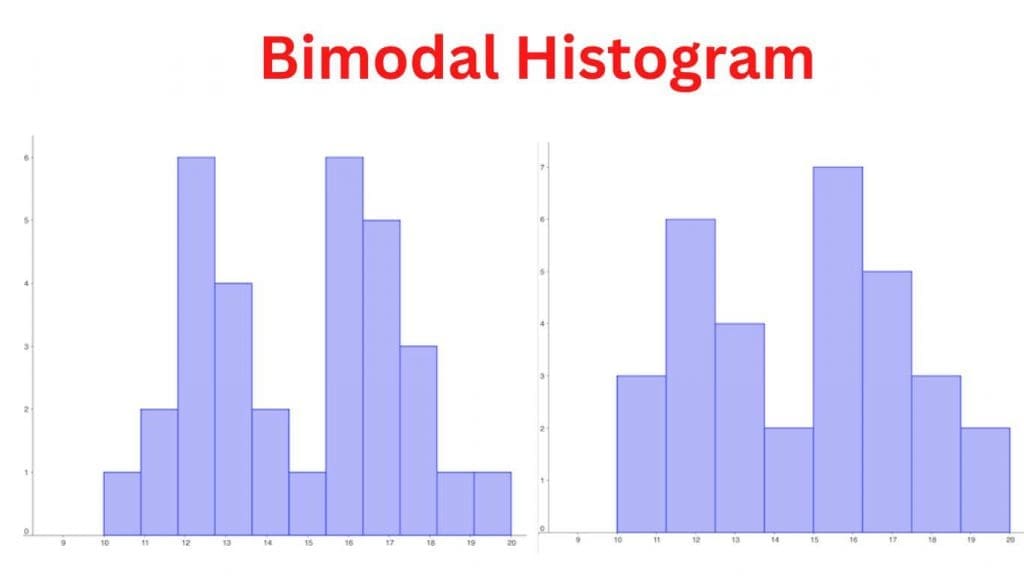
A bimodal distribution is a graph that shows two distinct modes or peaks. A bimodal symmetric histogram, in other words, is a histogram that has two bumps or humps, vs a unimodal distribution shape has only one high point. Each peak represents different data categories or groups that can have different values or characteristics. Histogram bimodales are used to visualize data with two different sources or processes, as in statistics. They can give insight into the data’s nature and identify trends, patterns, or anomalies.
How to Create a Bimodal Histogram
You will need two modes of data to create a bimodal Histogram. The steps for creating a bimodal Histogram are:
- Collect data: To collect data, you will need to have a collection of data with two distinct modes. The data can either be continuous or categorical.
- Select your bin width. Bin width is what determines the size of the bars on the histogram. A smaller bin will give more detail, but may also result in an untidy-looking histogram.
- Calculate the frequency by dividing the data range into bins with equal width and counting the number of observations in each bin.
- Drawbars: Draw an equal height bar above each bin.
- Identify modes: Look for two distinct peaks on the histogram. The position and height of the peaks can give you a clue as to the data’s nature.
- Label axes. Label the x-axis variable and y-axis frequency or relative frequency.
- Add a title: Give the histogram an informative title that summarizes both the data and modes.
- Analyze your results: Use a bimodal histogram in order to identify trends, patterns, or anomalies. Histograms can be used to compare two modes and make informed decisions about the data.
Bimodal Histogram Applications
Bimodal Symmetric Histograms can be used in many different fields and applications. Here are a few examples:
- Genetics: Bimodal histograms can be used to identify gene expression levels and two distinct groups that are active in different conditions. This information can help identify new disease pathways or drug targets.
- Marketing: Bimodal histograms are useful for analyzing customer satisfaction levels and identifying two distinct groups with different levels. This information can inform marketing and customer service strategies.
- Finance: Bimodal histograms can be used to analyze stock prices and other financial indicators. They can give investors insight into the behavior and trends of the stock exchange, and they can help them make informed decisions.
- Manufacturing: Bimodal histograms can be used to analyze product defects, and identify two distinct defect groups that could be caused by a variety of factors. This information can help improve product quality by reducing defects.
- Education: Bimodal histograms can be used to analyze test scores of students and identify groups with different levels. This information can help identify students who may require additional support or enrichment.
- Psychology: Bimodal histograms can be used to identify and analyze two distinct groups with different personalities. These data can be used for developing personalized treatments or interventions.
What Causes Bimodal Distributions?
Understanding that your data is distributed in a symmetric bimodal histogram way will help you to better understand the topic of your study. This distribution type usually has a reason for its existence. Here are some examples.
Merging two processes or populations
Combining two processes or populations into one dataset can produce a bimodal pattern. Each of the conditions has its own mode. Combining them will give you two modes.
Imagine, for example, that you are weighing adult black bears. You can see two peaks in the distribution of data when you graph it. The average female black bear weighs 175 pounds, while males average 400. Each average corresponds with a peak in the distribution. One peak corresponds to females, and the other to males.
Bimodal vs. Unimodal Distribution
Definition
A distribution’s modality can either be Unimodal or Bimodal, depending on how often the values occur. Unimodal distributions are single-peak distributions, where one value is more frequent than all the others. A distribution that has a clearly visible peak, or the most frequent value. A bimodal distribution is one where the two most frequent values are separated with a gap.
Shape
In unimodal distribution, the distribution shape has only one high point. The high point can be in the middle, or it may peak to the right or left. The mode is the highest value that is most often observed in the data. A bimodal distribution is one that has two high points or modes. The two modes usually have a large gap between them and the distribution has more data.
What Causes Bimodal distributions?
Understanding that your data are distributed in a bimodal way will help you to better understand the topic of your study. This distribution type usually has a reason for its existence.
Merging two processes or populations
Combining two processes or populations into one dataset can produce a bimodal pattern. Each of the conditions underlying it has its own mode. Combining them will give you two modes.
Imagine, for example, that you are weighing adult black bears. You can see two peaks in the distribution of data when you graph it. The average female black bear weighs 175 pounds, while males weigh 400 pounds. Each average corresponds with a peak in the distribution. One peak corresponds to females, and the other to males.
Bimodal distributions are often caused by differences between genders. Imagine you are measuring the strength of a product from an assembly line and notice that there is a bimodal pattern. You find out that one shift is using a slightly modified procedure which produces a weakened product. Both processes produce dual peaks.
Natural Bimodal Distributions
In some cases, the distributions of phenomena you are studying are bimodal. The size of Weaver worker ants and the age at which Hodgkin’s Lymphoma first appears are two examples of bimodal distribution.
You can’t break down a bimodal distribution to separate unimodal ones in these cases. Understanding the bimodal nature of your study area will help you to better understand it and identify the most common values near the two peaks.
Analysis of Bimodal Distributions
Bimodal distributions are rare, but it’s important to recognize them when they do. It’s a valuable discovery to discover that your data follows a bimodal pattern when you are working with combined populations or conditions. You have identified a variable that affects the result. This variable can be used by you and other scientists in future research.
This process allows you to obtain more accurate measures for variability and better measures for central tendency. Unreliable results can result from failing to take into account the different distributions. The mean and mode of a symmetric bimodal histogram are often not near the most commonly used values.
How have you applied Bimodal Histograms to your projects?
Tell us in the comments below!












