Stability of a Measurement System

Measurement system stability refers to the consistent performance of measuring equipment, operators, and procedures over extended time periods. Unlike repeatability studies that focus on short-term variation, stability assessment evaluates whether measurement bias remains constant or changes systematically over weeks, months, or years.

Stability specifically examines changes in measurement bias over time, distinguishing it from other measurement system analysis components. This temporal perspective reveals gradual deterioration, seasonal effects, or systematic drift that shorter studies might miss entirely.

Furthermore, stability encompasses multiple dimensions including calibration drift, environmental sensitivity, operator consistency, and equipment wear patterns. Each dimension contributes to overall measurement uncertainty and requires specific monitoring approaches to maintain system integrity over time.

What is the Stability of a Measurement System?

The stability of a measurement system refers to the ability of a measurement tool or process to produce consistent results over an extended period under identical conditions.

Think of it as the steady heartbeat of your quality control process—reliable, predictable, and unwavering. Stability is a critical component of Measurement System Analysis (MSA), a methodology used to evaluate the performance of measurement systems, particularly in frameworks like Six Sigma and Gage R&R studies.

A stable measurement system ensures that variations in data come from the process itself, not from fluctuations in the measurement tool. For example, a thermometer used in a lab must consistently measure the same temperature for a controlled sample, regardless of when or how often it’s used. Without stability, you risk making decisions based on faulty data, leading to costly errors.

Why Stability Matters in Quality Control?

Stability is the foundation of trust in any measurement-driven process. Here’s why it’s so critical:

• Consistency: Stable systems deliver repeatable results, ensuring data reliability.
• Accuracy: Stability supports accurate measurements, reducing the risk of defective products.
• Cost Savings: By minimizing measurement errors, you avoid rework, scrap, and recalls.
• Compliance: Industries like pharmaceuticals and aerospace require stable measurements to meet strict regulatory standards.

In short, measurement system stability is the glue that holds quality assurance together, enabling data-driven decisions with confidence.

Key Components of Measurement System Stability

To understand stability, you need to grasp its role within Measurement System Analysis. Stability is one of several attributes evaluated in MSA, alongside accuracy, precision, repeatability, and reproducibility. Let’s break down how stability fits into this framework:

1. Stability vs. Accuracy: While accuracy measures how close a measurement is to the true value, stability focuses on consistency over time.
2. Stability vs. Precision: Precision refers to the closeness of repeated measurements, while stability ensures those measurements remain consistent across days, weeks, or months.
3. Stability in Gage R&R: In Gage Repeatability and Reproducibility (Gage R&R) studies, stability ensures that measurement variations stem from the process, not the tool.

By maintaining stability, you create a solid foundation for other MSA attributes, ensuring your measurement system performs reliably.

How to Assess Measurement System Stability?

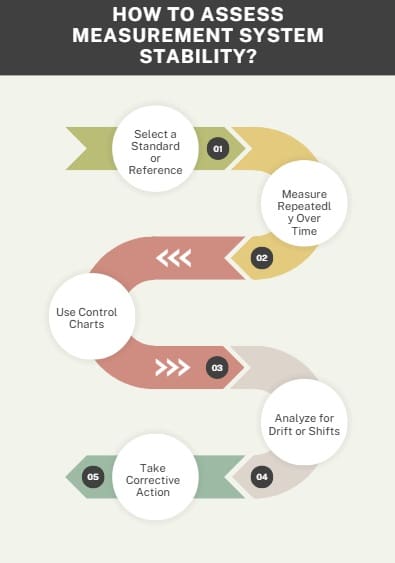
Assessing stability in a measurement system involves monitoring its performance over time to detect any drift or shifts in measurement output. Here’s a step-by-step guide to evaluating stability:

1. Select a Standard or Reference

Choose a stable, known reference sample (e.g., a certified weight or a standard part) with a consistent true value. This serves as your benchmark for repeated measurements.

2. Measure Repeatedly Over Time

Conduct multiple measurements of the reference sample at regular intervals—daily, weekly, or monthly, depending on your process. Use the same operator, equipment, and conditions to isolate the measurement system’s performance.

3. Use Control Charts

Plot the measurement results on a control chart, such as an X-bar and R chart or an Individuals and Moving Range (I-MR) chart. These charts help you visualize trends, drifts, or sudden shifts in measurements.

• X-bar Chart: Tracks the average measurement over time.
• R Chart: Monitors the range of measurements to detect variability.

If the measurements stay within control limits (typically ±3 standard deviations), the system is stable. Out-of-control points indicate potential instability.

4. Analyze for Drift or Shifts

Look for patterns in the control chart:

• Drift: A gradual change in measurements over time, often due to equipment wear or calibration issues.
• Shifts: Sudden changes in measurement output, possibly caused by environmental factors or equipment failure.

5. Take Corrective Action

If instability is detected, investigate root causes—worn parts, improper calibration, or environmental changes (e.g., temperature fluctuations). Address these issues to restore stability.

Also Read: Measurement System Analysis (MSA)

Example

Imagine a factory using a digital caliper to measure the diameter of a metal rod. To assess stability, the quality team measures a standard rod (known diameter: 10 mm) daily for 30 days. The results are plotted on an X-bar and R chart. If the measurements hover around 10 mm with minimal variation and no out-of-control points, the caliper is stable.

However, if the measurements drift upward to 10.2 mm over time, the team must investigate potential causes, such as tool wear or improper handling.

Factors Affecting Measurement System Stability

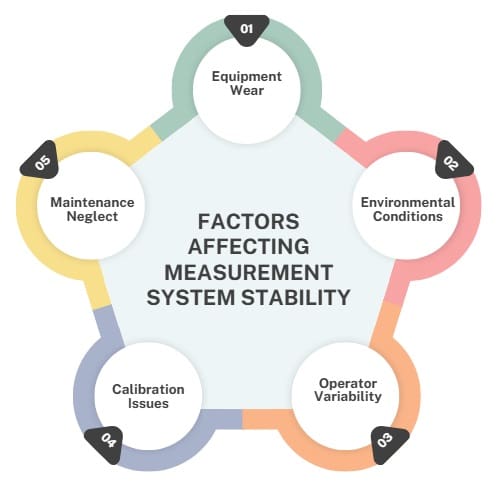
Several factors can disrupt the stability of a measurement system. Understanding these helps you proactively maintain reliability:

• Equipment Wear: Over time, tools like gauges or sensors may degrade, leading to inconsistent measurements.
• Environmental Conditions: Temperature, humidity, or vibrations can affect measurement accuracy.
• Operator Variability: Inconsistent techniques or lack of training can introduce errors.
• Calibration Issues: Infrequent or improper calibration can cause measurement drift.
• Maintenance Neglect: Failing to maintain equipment (e.g., cleaning or lubrication) can compromise stability.

By addressing these factors, you can safeguard the reliability of measurement systems and ensure consistent performance.

Best Practices for Maintaining Measurement System Stability

To keep your measurement system stable, adopt these practical strategies:

1. Regular Calibration: Schedule routine calibration to ensure tools align with standards. For example, calibrate a pressure gauge every six months to maintain accuracy.
2. Control Environmental Factors: Maintain consistent temperature, humidity, and lighting in measurement areas.
3. Train Operators: Provide comprehensive training to ensure consistent measurement techniques.
4. Use Preventive Maintenance: Regularly inspect and service equipment to prevent wear-related instability.
5. Monitor with Control Charts: Continuously track measurement data to catch issues early.
6. Standardize Procedures: Implement clear protocols for measurement processes to minimize variability.

By following these practices, you’ll enhance the consistency of measurement systems and reduce the risk of errors.

Also Read: What is PPM (Parts Per Million) Measurement?

Stability in Different Industries

The importance of measurement system stability varies across industries, but its impact is universal:

• Manufacturing: Stable measurements ensure product quality, reducing defects in automotive parts or electronics.
• Healthcare: In medical labs, stable instruments like blood analyzers ensure accurate diagnoses.
• Aerospace: Precision measurements in aircraft components rely on stable systems to meet safety standards.
• Pharmaceuticals: Stability in measurement systems ensures consistent drug formulations, critical for patient safety.

In Six Sigma projects, stability is a cornerstone of the Measure phase, ensuring data reliability for process improvements.

Challenges and Limitations of Stability Assessment

While assessing stability in measurement systems is critical, it’s not without challenges:

1. Time-Intensive: Collecting data over weeks or months can be resource-heavy.
2. External Influences: Environmental changes or operator errors can skew results.
3. Subjectivity: Interpreting control charts requires expertise to avoid misdiagnosis.
4. Cost: Maintaining stable systems through calibration and maintenance can be expensive.

To overcome these, invest in automated measurement systems, robust training, and statistical software to streamline stability assessments.

Tools and Technologies for Stability Analysis

Modern tools can simplify the process of ensuring measurement system stability:

• Statistical Software: Tools like Minitab or JMP generate control charts and analyze stability data.
• Automated Measurement Systems: Devices with built-in diagnostics reduce human error.
• IoT Sensors: Real-time monitoring of environmental conditions helps maintain stability.
• Calibration Management Software: Tracks calibration schedules to prevent drift.

By leveraging these technologies, you can enhance the reliability of measurement systems and streamline quality control.

FAQs About Stability of a Measurement System

What is the stability of a measurement system?

Stability refers to a measurement system’s ability to produce consistent results over time under identical conditions, a key component of Measurement System Analysis (MSA).

How do you assess measurement system stability?

Use a reference standard, measure repeatedly over time, and plot results on a control chart (e.g., X-bar and R chart) to detect drift or shifts.

Why is stability important in quality control?

Stability ensures reliable, repeatable measurements, reducing errors, ensuring compliance, and supporting data-driven decisions in processes like Six Sigma.

What factors affect measurement system stability?

Equipment wear, environmental conditions, operator variability, and improper calibration can disrupt stability, leading to inconsistent measurements.

How does stability relate to Gage R&R?

In Gage R&R studies, stability ensures measurement variations reflect the process, not the tool, supporting accurate repeatability and reproducibility.

Final Words

The stability of a measurement system is the unsung hero of quality control, ensuring your data remains trustworthy over time. By assessing stability with tools like control charts, addressing factors like equipment wear, and adopting best practices like regular calibration, you can maintain consistent measurement systems that drive success.

Whether you’re in manufacturing, healthcare, or aerospace, mastering stability empowers you to make informed decisions, reduce defects, and meet regulatory standards.

Related Articles

• Drift
• Calibration
• Common Cause Variation
• Measurement System Analysis (MSA)
• Capability