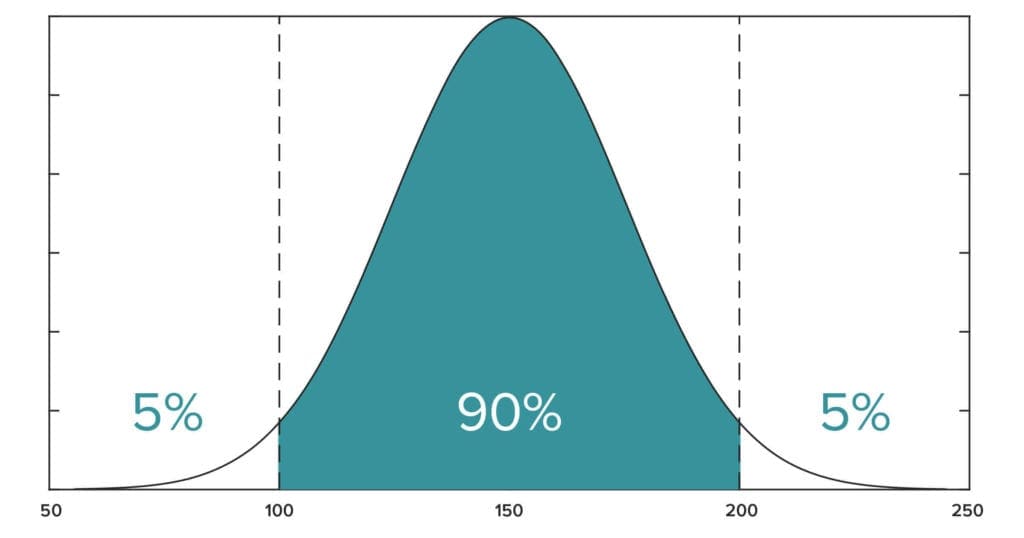
In statistics, a confidence interval (CI) is a type of estimate computed from the statistics of the observed data. It is a range describing where the true population parameter lies with a certain degree of confidence. For example, a 95% confidence interval for the mean estimates that the true mean lies within the confidence interval with 95% confidence (with 5% alpha risk). The interval has an associated confidence level that gives the probability with which an estimated interval will contain the true value of the parameter. The confidence level is chosen by the investigator. For a given estimation in a given sample, using a higher confidence level generates a wider (i.e., less precise) confidence interval. In general terms, a CI for an unknown parameter is based on sampling the distribution of a corresponding estimator.
This means that the confidence level represents the theoretical long-run frequency (i.e., the proportion) of confidence intervals that contain the true value of the unknown population parameter. In other words, 90% of CIs computed at the 90% confidence level contain the parameter, 95% of CIs computed at the 95% confidence level contain the parameter, 99% of CIs computed at the 99% confidence level contain the parameter, etc.
The confidence level is designated before examining the data. Most commonly, a 95% confidence level is used. However, other confidence levels, such as 90% or 99%, are sometimes used.
Factors affecting the width of the CI include the size of the sample, the confidence level, and the variability in the sample. A larger sample will tend to produce a better estimate of the population parameter, when all other factors are equal. A higher confidence level will tend to produce a broader confidence interval.
References
Wikipedia. https://en.wikipedia.org/wiki/Confidence_interval