Regression Equation

In statistics, a regression equation is a tool used to model the relationship between two or more variables. It helps us understand how the dependent (response) variable changes when the independent (explanatory) variable changes. In simple terms, a regression equation is like a formula that predicts one value based on another.

What is a Regression Line?

A regression line is a straight line that shows the relationship between two variables. The line shows how the response variable (Y) changes when the explanatory variable (X) changes. When we plot data points on a scatterplot, a regression line often appears to be a good fit, even if some data points don’t lie exactly on the line.

In regression analysis, the goal is to find the best-fit line. This line minimizes the difference between the actual data points and the predicted values. Once the line is drawn, we can use it to make predictions about the response variable for any given value of the explanatory variable.

How Does Regression Analysis Work?

Regression analysis is the process of finding the regression line. The line is calculated based on data points, which are the values of both the independent and dependent variables. A software program can help compute this line accurately, but understanding the math behind it is essential.

For example, consider a student’s GPA and self-esteem score. If we want to predict a student’s self-esteem based on their GPA, the regression line helps make this prediction. The line shows how self-esteem changes with each point increase in GPA.

Regression Equation

A regression equation in statistics describes the relationship between a dependent variable (Y) and independent variables (X1, X2,…, Xk). It helps predict the value of Y based on the values of X.

To select the best regression equation, consider two factors:

1. Include as many variables (Z’s) as possible to reduce bias.
2. Minimize the number of Z’s to reduce variance and cost.

Several methods can help choose the best equation:

• All possible regressions.
• Forward selection.
• Backward elimination.
• Stepwise regression.

In the method of all possible regressions, every possible regression equation is tested. If there are r predictors, 2^r possible equations can be formed. The best equation is one with:

1. High R² and adjusted R² values and fewer predictors.
2. A Cp statistic close to the number of predictors.

Simple Linear Regression Equation

A simple linear regression equation is written as: E(y) = b0 + b1x

• E(y) is the predicted value of y for a given x.
• b0 is the y-intercept.
• b1 is the slope of the line.
  A positive slope (b1) shows a positive relationship between x and y. A negative slope (b1) shows a negative relationship. If the slope is zero, there is no relationship between x and y.

Estimated Simple Linear Regression Equation

The estimated equation is: ŷ = b0 + b1x Where ŷ is the estimated value of y for a given x.

Regression Lines

There are two regression lines:

Regression of Y on X: This predicts Y for a given X.
Formula: Y = a + bX

Regression of X on Y: This predicts X for a given Y.
Formula: X = a + bY

Here, a is the intercept and b is the slope (regression coefficient). These constants determine the position and slope of the line.

Method of Least Squares

The values of a and b are found using the least squares method. This involves solving normal equations. The form of these equations depends on whether you’re solving for Y on X or X on Y.

Regression Coefficients

The regression coefficient b represents the slope of the regression line. There are two types:

• bxy: Regression coefficient of X on Y.
• byx: Regression coefficient of Y on X.

These coefficients can be calculated using various methods, including correlation coefficients and standard deviations.

Properties of Regression Coefficients

• The correlation coefficient r is the geometric mean of bxy and byx.
• If one regression coefficient is greater than one, the other must be less than one.
• Both regression coefficients have the same sign (both positive or both negative).
• The average of the two coefficients is greater than the correlation coefficient.
• Regression coefficients are independent of origin but not scale.

Regression Equation Formula

The regression equation is a mathematical formula that predicts the value of the dependent variable based on the independent variable. It is written as:

The regression equation helps us understand the relationship between X and Y. For example, in the case of predicting self-esteem based on GPA, the equation might look like this:

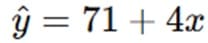
Here, 71 is the intercept, and 4 is the slope. This means that for each point increase in GPA, the self-esteem score increases by 4 points. If a student has a GPA of 2.0, we can use the equation to predict their self-esteem score:

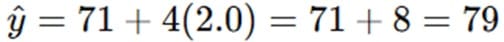
So, a student with a GPA of 2.0 is predicted to have a self-esteem score of 79.

Importance of the Regression Line

The regression line is essential because it provides a clear, predictable relationship between variables. In simple cases, the line helps predict one variable (Y) based on another (X). For instance, by knowing a student’s GPA, we can predict their self-esteem score using the regression equation.

However, the regression line does not guarantee that the predicted values will be exact. Most of the time, data points are scattered around the line. The line represents the average relationship, and the actual values might be a little higher or lower than the predictions.

Identifying Dependent and Independent Variables

In regression analysis, it is important to distinguish between the dependent and independent variables. The dependent variable is the one you are trying to predict, while the independent variable is used to explain or predict changes in the dependent variable.

For example, in the self-esteem and GPA example, self-esteem is the dependent variable (Y), and GPA is the independent variable (X). The regression equation shows how self-esteem depends on GPA.

Sometimes, we might switch the dependent and independent variables, which changes the regression equation. If we want to model GPA based on self-esteem, the roles of X and Y would switch.

Types of Regression

1. Simple Regression: This type of regression involves one independent variable and one dependent variable. The regression equation shows how changes in the independent variable affect the dependent variable.
2. Multiple Regression: In multiple regression, there are multiple independent variables. This allows us to model more complex relationships. For example, we could use both GPA and the number of study hours as independent variables to predict self-esteem.

Origin of the Term “Regression”

The term “regression” comes from a study on the relationship between the height of fathers and sons. It was observed that very tall fathers tended to have sons who were shorter than them, and very short fathers had sons who were taller than them.

This phenomenon was called “regression toward the mean.” It suggested that extreme values in a population tend to be followed by more average values.

Linear Relationship Between Variables

The simplest form of regression is a linear relationship, where one variable (Y) is related to another variable (X) in a straight line. The equation for this relationship is:

Stochastic Model for Real-Life Data

In many real-life situations, the relationship between variables is not perfectly deterministic (i.e., the same X always leads to the same Y). Instead, there is some randomness involved. For example, even if income remains the same, consumption patterns may vary.

To account for this randomness, we use a stochastic model, which includes an error term (e). The regression equation then becomes:

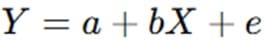
Here, e represents the random error or variation that cannot be explained by the independent variable.

Fitting a Regression Line

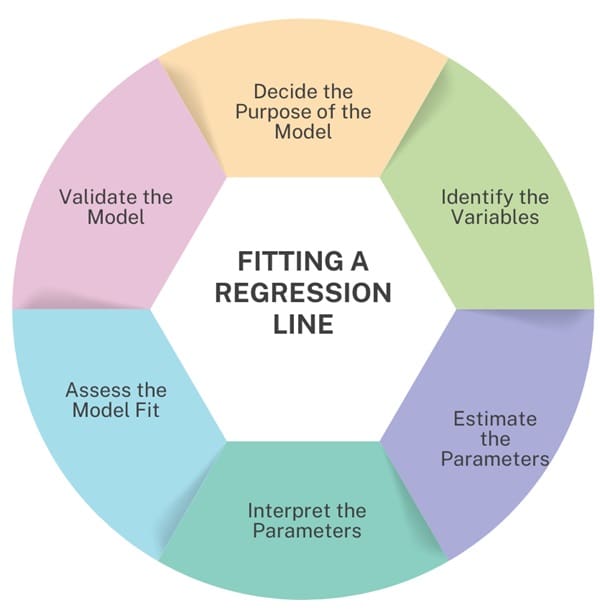
To fit a regression line to data, follow these steps:

1. Decide the Purpose of the Model: Understand the goal of your analysis. What are you trying to predict?
2. Identify the Variables: Choose the dependent and independent variables based on your research question.
3. Estimate the Parameters: Use statistical methods to estimate the intercept (a) and slope (b).
4. Interpret the Parameters: Analyze the results to understand the relationship between the variables.
5. Assess the Model Fit: Check how well the regression line fits the data.
6. Validate the Model: Test the regression equation on new data to confirm its accuracy.

Practical Example

Let’s take the example of rainfall and agricultural production. If we have data on rainfall and crop yield for several years, we can use regression analysis to predict crop yield based on the amount of rainfall. The regression equation might look like this:

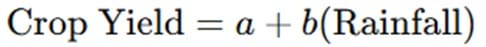
This equation would allow us to estimate the crop yield for a given amount of rainfall.

Example

Given the data:
X: 10, 12, 16, 11, 15, 14, 20, 22
Y: 15, 18, 23, 14, 20, 17, 25, 28

Step 1: Calculating Required Values

Final Words

A regression equation is a powerful tool for understanding and predicting the relationship between variables. Whether in simple linear regression or more complex multiple regression, the goal is to model how changes in one variable affect another.

By using regression analysis, we can make more informed decisions based on data and predict outcomes more accurately. Understanding how to compute and interpret regression equations is essential for anyone working with data in fields like economics, medicine, and social sciences.

Related Articles

• What Is Multiple Linear Regression (MLR)?
• Multiple Regression
• Multiple Linear Regression
• Simple Linear Regression
• LSSGB-O Module #14 – Correlation & Regression Analysis​