In statistics and probability theory, the median is the value separating the higher half from the lower half of a data sample, a population, or a probability distribution. For a data set, it may be thought of as “the middle” value. The basic feature of the median in describing data compared to the mean (often simply described as the “average”) is that it is not skewed by a small proportion of extremely large or small values, and therefore provides a better representation of a “typical” value.
Some Examples:
Median income, for example, may be a better way to suggest what a “typical” income is, because income distribution can be very skewed.
The median of a finite list of numbers is the “middle” number, when those numbers are listed in order from smallest to greatest. If the data set has an odd number of observations, the middle one is selected. For example, the following list of seven numbers,
- 1, 3, 3, 6, 7, 8, 9
has the median of 6, which is the fourth value.
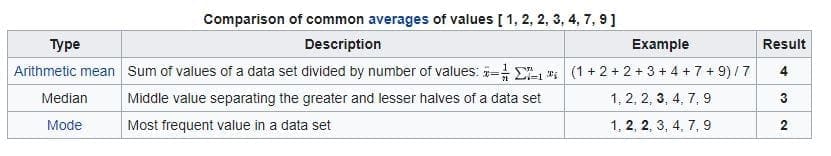
The median is well-defined for any ordered (one-dimensional) data, and is independent of any distance metric. It can thus be applied to classes which are ranked but not numerical, although the result might be halfway between classes if there is an even number of cases.
Notation
There is no widely accepted standard notation for this metric, but some authors represent the median of a variable x either as x͂ or as μ1/2 sometimes also M. In any of these cases, the use of these or other symbols for the median needs to be explicitly defined when they are introduced.
References
Wikipedia. Median https://en.wikipedia.org/wiki/Median
Related SSDSI Articles:


















