Monte Carlo Simulation

Monte Carlo Simulation (MCS) is a widely used mathematical technique. It relies on repeated random sampling to solve complex problems, estimate outcomes, and provide insight into uncertainty.

The method is named after the famous Monte Carlo casino in Monaco. This name reflects its reliance on random processes akin to gambling. MCS allows users to account for risk in quantitative analyses and decision-making, spanning diverse fields such as engineering, finance, physics, biology, and project management.

In essence, MCS provides a way to understand the range of potential outcomes from an event or process and the likelihood of each outcome occurring. It is particularly useful in situations where deterministic methods fail, as it allows the modeling of systems with a high degree of complexity or uncertainty.

This article explores the Monte Carlo simulation, starting with the classic Monty Hall problem, and delves into applications, probability distributions, methodology, and its advantages in various fields.

Monty Hall Problem (Khullja Sim Sim)

To understand MCS, let’s begin with a classic example known as the Monty Hall problem. Imagine you are on a game show and asked to choose between three doors. Behind one door is a car (the prize), while behind the other two are goats.

After you select a door, the host (Monty Hall), who knows what’s behind each door, opens one of the two doors you didn’t pick, revealing a goat. Monty then gives you a choice: you can either stick with your original door or switch to the other unopened door. What should you do?

Intuition may lead many to believe that switching doors doesn’t affect your chances of winning. However, MCS reveals a surprising result. If you don’t switch, the probability of winning is 1/3, whereas if you switch, the probability increases to 2/3. Simulate the game multiple times to demonstrate this counterintuitive conclusion. MCS performs this exact simulation.

Repeat the Monty Hall experiment thousands of times (e.g., 10,000 repetitions). Record the outcomes of each repetition. By observing how often switching leads to a win versus sticking with the original choice, we can empirically estimate the probabilities.

The results show that switching leads to a win about 66.8% of the time, while not switching leads to a win about 33.2% of the time.

What is Monte Carlo Simulation?

Monte Carlo simulation is a powerful statistical technique that leverages repeated random sampling to predict the outcomes of complex processes. The concept of random experiments closely ties to this idea. Outcomes in random experiments are uncertain and cannot be predicted in advance.

This simulation method allows us to perform “what-if” analyses, helping us understand potential outcomes by testing different scenarios based on random inputs.

Monte Carlo methods, broadly, involve using random sampling to estimate numerical results. In the context of the Monty Hall problem, we simulated the game repeatedly to estimate the probabilities of winning by switching versus not switching. Running multiple experiments to estimate an outcome is referred to as Monte Carlo simulation.

Researchers commonly use MCS when solving a problem analytically is impractical or impossible. By randomly generating inputs and analyzing the resulting outputs, MCS provides a numerical solution to the problem. The method has wide-ranging applications, from calculating integrals to simulating stock market fluctuations or determining the reliability of engineering systems.

Monte Carlo Simulation in Action: Rolling Dice Example

Consider another simple example: rolling two dice. The goal is to calculate the probability of the dice summing to a particular number, say seven. While we can manually calculate the probability (there are six combinations that sum to seven out of 36 possible combinations, so the probability is 6/36 or 0.167), MCS provides an alternative method.

In an MCS, we simulate rolling the dice many times (e.g., 10,000 times), record the sum of each roll, and then calculate how often the sum equals seven. As the number of simulations increases, the result will converge to the true probability (0.167). This demonstrates how MCS can approximate probabilities by random sampling.

How Monte Carlo Simulation Works?

Monte Carlo simulation performs risk analysis by constructing models of possible outcomes, incorporating uncertainty. Represent each input factor with inherent variability using a probability distribution. Run the simulation through numerous iterations (hundreds or thousands), using random values from those distributions.

Each iteration represents a possible outcome based on the sampled values, and by analyzing the range of outcomes over many iterations, MCS provides a distribution of results, offering insights into the probabilities of various scenarios occurring.

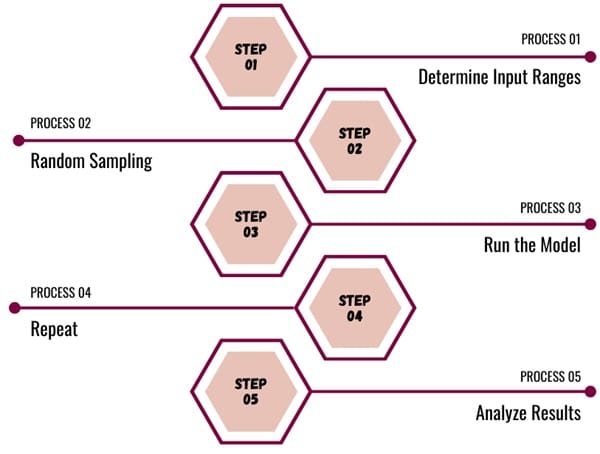
The Monte Carlo simulation process involves these steps:

1. Determine Input Ranges: First, define the possible range of input values based on historical data, expert knowledge, or educated guesses. This could include the range of time required to complete each project phase or the potential range of returns on an investment.
2. Random Sampling: Select random values for each input once the input ranges are defined. You can use probability distributions like normal, uniform, or triangular distributions, depending on the nature of the data.
3. Run the Model: Run the model using the randomly selected inputs. Record the results after each run.
4. Repeat: Repeat the process multiple times (often thousands), each time with different random input values.
5. Analyze Results: Compile the results after all iterations are complete. Analyze the data to gain insights into the likelihood of various outcomes.

For example, if you are estimating the total time for a construction project with three phases, you might estimate each phase to take between 3 to 7 months. Monte Carlo simulation will randomly pick different time values for each phase and calculate the total time for the project over hundreds or thousands of iterations. The results will help you determine the likelihood of completing the project within a specific time frame.

Key Concepts in Monte Carlo Simulation

Before diving into the methodology, it is important to understand some key concepts used in Monte Carlo simulations:

• Statistical Distributions: These describe how a random variable behaves. There are two types: discrete distributions (e.g., binomial, Poisson) and continuous distributions (e.g., normal, exponential). Monte Carlo simulations rely on these distributions as their foundation. These distributions define how to select random input variables.
• Random Sampling: Select random values from the population of possible input values. Ensure that each value has an equal chance of being chosen.
• Random Number Generators (RNG): These are tools used to create sequences of numbers that mimic random sampling. While RNGs are not truly random, they generate numbers that pass statistical tests and are sufficient for most simulations.

Using Probability Distributions

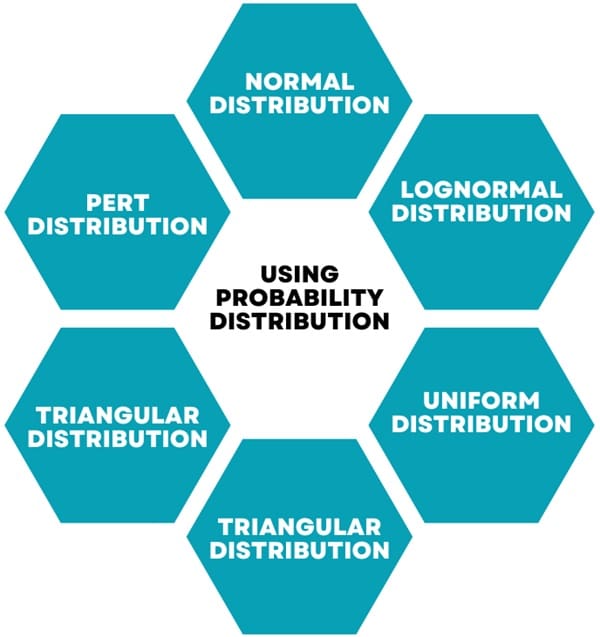
One of the key aspects of MCS is the use of probability distributions to represent uncertain variables. Different types of distributions can be used depending on the nature of the variable:

• Normal distribution: Also known as the bell curve, where values near the mean are most likely, and extreme values are less likely. This distribution is commonly used for variables like height, inflation rates, and energy prices.
• Lognormal distribution: Used for variables that cannot go below zero but have unlimited positive potential, such as stock prices or property values.
• Uniform distribution: All values within a range are equally likely. For example, manufacturing costs or future sales revenue can follow a uniform distribution.
• Triangular distribution: Defined by minimum, most likely, and maximum values, often used to model variables with a known range and central tendency, such as sales history or inventory levels.
• PERT distribution: Similar to the triangular distribution but gives less emphasis to extreme values. It’s often used in project management to estimate task durations.
• Discrete distribution: Specifies particular values and their probabilities, such as the outcome of a lawsuit (e.g., 20% chance of winning, 30% chance of losing, 50% chance of settling).

Monte Carlo Simulation Methodology

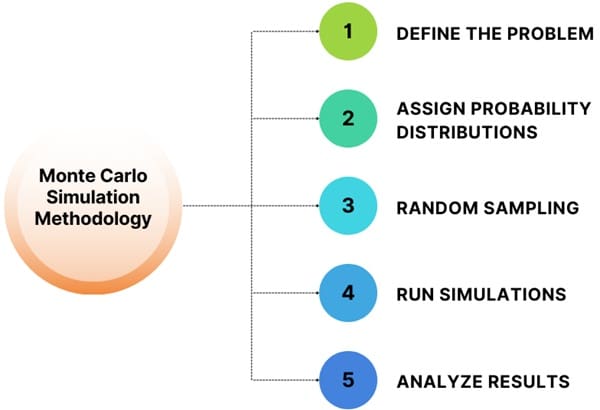
1. Define the Problem: Start by identifying the system or process that involves uncertainty and the output you wish to measure.
2. Assign Probability Distributions: For each input factor that involves uncertainty, assign an appropriate probability distribution based on historical data, expert judgment, or theory.
3. Random Sampling: Generate random samples from the input probability distributions.
4. Run Simulations: Run the simulation for a large number of iterations. Each iteration uses a different random sample to generate an output.
5. Analyze Results: Once the simulation has run enough iterations, analyze the distribution of outcomes. This provides a range of possible scenarios and their associated probabilities.

Applications of Monte Carlo Simulation

MCS is applied across various fields where uncertainty is a key factor:

• Engineering: MCS is used to estimate the reliability of complex systems, such as aircraft engines, bridges, or power grids. By simulating different operating conditions and component failures, engineers can assess system reliability and safety.
• Finance: Use MCS widely in finance to model stock prices, assess portfolio risks, and estimate the potential outcomes of investment strategies. For instance, MCS can simulate how a portfolio might perform under different economic conditions.
• Project Management: MCS helps project managers estimate task durations and project timelines. By modeling the uncertainty in task completion times, MCS can predict project completion dates and the likelihood of meeting deadlines.
• Climate Science: MCS is employed to model the behavior of complex climate systems. By simulating different scenarios with varying environmental factors, scientists can assess the potential impact of climate change.
• Biology: In biological research, MCS is used to model population dynamics, disease spread, and drug interactions. By simulating different conditions, researchers can gain insights into biological processes and make predictions.
• Quantum Physics and Particle Physics: Monte Carlo methods are critical for simulating particle interactions and behavior in high-energy physics experiments.

Also See: Lean Six Sigma Certification Programs, Arlington, Texas

Example: Birthday Candle Problem

Another intriguing example is the Birthday Candle problem. Imagine you have a birthday cake with 30 candles. Every time you blow on the candles, you randomly extinguish between 1 and the number of remaining candles. How many times do you have to blow before all the candles are out?

Using MCS, we can simulate this process multiple times to estimate the average number of blows required. The results of the simulation can then be averaged to approximate the expected number of attempts.

Advantages of Monte Carlo Simulation

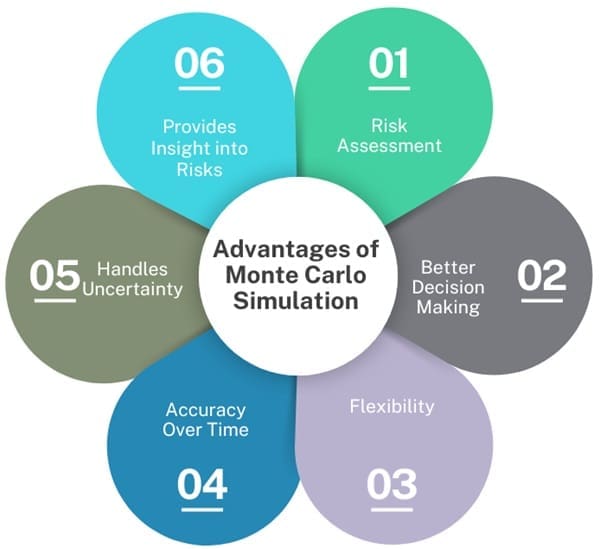
1. Risk Assessment: Monte Carlo simulation helps quantify risk by providing the probability of different outcomes. This is particularly important in fields like finance, where uncertainty in investment returns can significantly impact profitability.
2. Better Decision Making: By simulating a wide range of potential outcomes, decision-makers can better plan for future uncertainties. In project management, for example, knowing the likelihood of meeting deadlines or staying within budget allows for more informed choices regarding resource allocation, risk mitigation, and contingency planning.
3. Flexibility: Apply Monte Carlo simulations across a wide variety of fields and industries. Adapt the methodology to suit the particular model, whether you are estimating financial returns, forecasting project timelines, or analyzing cost risks.
4. Accuracy Over Time: The more times a Monte Carlo simulation is run, the more accurate the results become. By running the model hundreds or thousands of times, it averages out the random errors that may occur in any single trial, producing a more reliable overall forecast.
5. Handles Uncertainty: MCS is highly effective for modeling systems with significant uncertainty. It provides a way to estimate outcomes when exact analytical solutions are not feasible.
6. Provides Insight into Risks: By running many simulations and analyzing the outcomes, MCS helps decision-makers understand the risks involved in different courses of action.

Challenges and Limitations

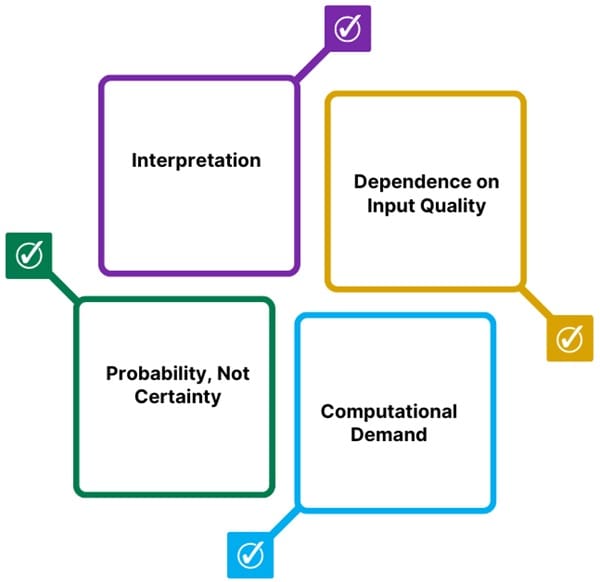
While MCS is a powerful tool, it has certain limitations:

• Interpretation: Interpreting the results of MCS requires a good understanding of probability and risk analysis, as the outcomes are expressed in probabilistic terms.
• Dependence on Input Quality: The accuracy of Monte Carlo simulations relies heavily on the quality of the input estimates. If your input ranges or probability distributions are inaccurate, the simulation results will also be unreliable.
• Computational Demand: Running thousands of iterations in Monte Carlo simulations can be computationally expensive and time-consuming, especially for complex models with numerous variables.
• Probability, Not Certainty: Monte Carlo simulations provide probabilities, not certainties. They can tell you how likely something is to happen, but they can’t guarantee that it will happen within the predicted range.

What Monte Carlo Simulation Can Reveal?

One of the key benefits of Monte Carlo simulation is its ability to show the probability of different outcomes. For instance, in project management, it can give insights into how likely the project is to meet a deadline or stay within a budget. In finance, it can simulate the probability of different returns on investment based on a range of market conditions.

Since the simulation runs hundreds or thousands of times, each time selecting random inputs based on the given ranges, it generates a wide array of potential outcomes. By analyzing these results, you can assess how likely various scenarios are, helping you better understand the inherent risk in the project or model.

Process of Monte Carlo Simulation

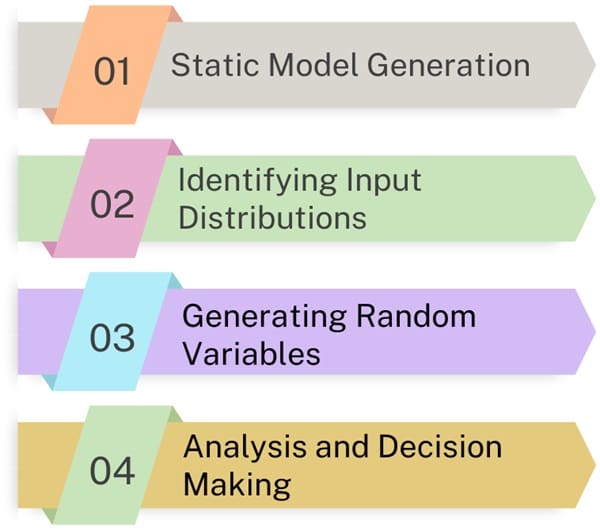
Monte Carlo simulations typically follow a step-by-step process that transforms a deterministic model into a stochastic model that accounts for uncertainties in input variables. The steps include:

1. Static Model Generation: The simulation starts with a deterministic model, using the most likely input values. This model closely resembles the real-world scenario and produces an initial set of output values.
2. Identifying Input Distributions: Establish the deterministic model first. Then, identify the statistical distributions that govern the input variables. Historical data can help determine these distributions, ensuring that they reflect the actual variability in the system.
3. Generating Random Variables: Once input distributions are defined, random samples are generated from each distribution. These random samples are fed into the deterministic model, creating new sets of output values.
4. Analysis and Decision Making: Collect a large number of output values after running multiple simulations. Analyze these results statistically to assess the range of potential outcomes and the associated risks.
   Decision-makers can use this information to make informed choices about the system being studied.

Practical Example

Let’s consider a simple example of a construction project with three jobs to be completed sequentially. Initially, we estimate each job to take 5, 4, and 5 months, respectively, for a total project duration of 14 months. This is a fixed estimate based on experience but doesn’t account for uncertainty.

Using Monte Carlo simulation, however, we could provide a range of estimates for each job. For instance:

• Job 1 might take between 4 and 7 months
• Job 2 might take between 3 and 6 months
• Job 3 might take between 4 and 6 months

Monte Carlo simulation randomly generates values within these ranges for each job and calculates the total project time. After running 500 simulations, the results might show that there’s only a 34% chance of finishing the project in 14 months or less, while there’s a 79% chance of finishing it in 15 months or less. These probabilities provide a more realistic assessment of the time required to complete the project.

Applications of Monte Carlo Methods

Don’t limit Monte Carlo methods to forecasting models. Apply them to a wide range of problems, especially when analytical or numerical solutions are difficult to obtain or implement.

1. Bayesian Analysis: In Bayesian statistics, Monte Carlo simulations can help compute posterior distributions when they don’t have a closed form. By generating random samples from the posterior distribution, you can estimate means or modes, which are used to infer the most likely outcomes.
2. Numerical Integration: Monte Carlo integration is another common application. It involves using random sampling to estimate the value of an integral, particularly useful in higher dimensions where traditional methods like Riemann Integration become inefficient.
3. Optimization: Monte Carlo methods can also be used in optimization problems. By randomly generating solutions and evaluating them, it’s possible to find the optimal solution to a complex problem without having to evaluate every single possibility exhaustively.

Software for Monte Carlo Simulation

There are numerous software tools available for performing Monte Carlo simulations. Some popular options include:

• @Risk (Palisade): This is an add-on for Microsoft Excel that allows users to perform risk analysis and Monte Carlo simulations directly in spreadsheets.
• MATLAB: MATLAB provides powerful tools for Monte Carlo simulations, particularly in engineering and scientific research.
• Crystal Ball (Oracle): Another Excel-based tool, Crystal Ball allows users to model uncertainties and perform risk analysis.
• Simul8: Industries such as manufacturing, healthcare, and logistics widely use this simulation software. They use it for optimizing processes.

Final Words

Monte Carlo simulation is a robust and flexible technique that is invaluable for risk analysis and decision-making in uncertain environments. From simple problems like rolling dice to complex systems like climate models and financial markets, MCS provides a way to model uncertainty, estimate outcomes, and assess risks.

By incorporating randomness and running simulations multiple times, MCS helps decision-makers gain insights into the range of possible scenarios and the likelihood of each one occurring. Despite its computational intensity, the benefits of MCS make it an essential tool in engineering, finance, project management, and beyond.

Related Articles

• Lean Zone® Production Methodologies
• The Lean Zone® Sub-Assembly Simulation
• Lean Zone® Office Simulation
• Random Sampling
• About Visionary Products USA Inc.