Arithmetic Mean

For a data set, the arithmetic mean, also known as average or arithmetic average, is a central value of a finite set of numbers: specifically, the sum of the values divided by the number of values. In colloquial language, an average is a single number taken as representative of a non-empty list of numbers. Different concepts of average are used in different contexts. In statistics, mean, median, and mode are all known as measures of central tendency, and in colloquial usage any of these might be called an average value.

While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly influenced by outliers (values that are very much larger or smaller than most of the values). For skewed distributions, such as the distribution of income for which a few people’s incomes are substantially greater than most people’s, the arithmetic mean may not coincide with one’s notion of “middle”, and robust statistics, such as the median, may provide better description of central tendency.

The arithmetic mean is the most commonly used and readily understood measure of central tendency in a data set. In statistics, the term average refers to any of the measures of central tendency. The arithmetic mean of a set of observed data is defined as being equal to the sum of the numerical values of each and every observation, divided by the total number of observations

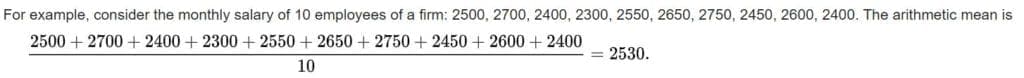
If the data set is a statistical population (i.e., consists of every possible observation and not just a subset of them), then the mean of that population is called the population mean, and denoted by the Greek letter $\mu$ (mu). If the data set is a statistical sample (a subset of the population), then we call the statistic resulting from this calculation a sample mean (which for a data set is denoted as ${\overline {X}}$ ).