What are the real uses of polynomials in real life? To predict and estimate the response shapes over a variety of input parameters, we use polynomial modeling. This model is a powerful tool to determine which input factors are driving responses and in which direction. These models are the most commonly used to analyze designed experiments. The equation below shows a quadratic polynomial model (second-order), for two explicatory variables. The main effects are the single x-terms. Quadratic effects are the squared terms. They are used to model curvature on the response surface. Cross-product terms can be used to model interactions among explanatory variables.
A polynomial model in real life uses a generalized notion of transfer functions to express the relationship between the input, u(t), the output y(t), and the noise e(t) using the equation:
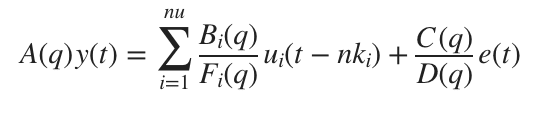
The variables A, B, and C are polynomials that are expressed in the time shift operator q-1. ui is ith input, nu the total number, and nki the delay at the ith input that defines the transport delay. Assume that the variance of white noise (e(t)) is l. Understanding Time-Shift Operator Q for more information.
They can also be used in real life in most engineering and manufacturing applications that only deal with second-order polynomial models. As we increase the number of explanatory variables, and thus the number of cross-product terms, equations can become more complex. We rarely see interaction terms beyond the two-factor level. This allows us to keep the equations manageable.
Multiple regression is a technique that fits the entire equation when the number of factors exceeds 5. Stepwise regression is used when the number of factors exceeds 5. Many statistical analysis programs can perform stepwise regression. Using a polynomial model in real life, you simply need to enter all the terms in the polynomial model and the software will choose the best terms to describe the data. This chapter provides examples and a detailed discussion on this topic.











