The Central Limit Theorem (CLT) stands as one of statistics’ most fundamental concepts. This powerful theorem explains how sample means behave when drawn from any population. Understanding CLT meaning helps statisticians make predictions about unknown populations using sample data.
Simply put, the central limit theorem states a remarkable fact. When you take multiple samples from any population, the sample means form a normal distribution. This happens regardless of the original population’s shape or distribution type.
Table of contents
What is the Central Limit Theorem?
The Central Limit Theorem, often called CLT, is a fundamental statistical concept. It states that the distribution of sample means approaches a normal distribution. This happens as the sample size grows, regardless of the population’s shape. In other words, if you take many samples and calculate their means, those means form a bell-shaped curve. This is true even if the population data is skewed or non-normal.
For example, imagine rolling a die. The outcomes are uniform, not normal. However, if you roll the die multiple times and average the results, the distribution of those averages becomes normal. This is the magic of CLT in action. It allows statisticians to make predictions about populations using sample data.
Public, Onsite, Virtual, and Online Six Sigma Certification Training!
- We are accredited by the IASSC.
- Live Public Training at 52 Sites.
- Live Virtual Training.
- Onsite Training (at your organization).
- Interactive Online (self-paced) training,
CLT Meaning and Definition
So, what does CLT stand for? CLT stands for Central Limit Theorem. Its definition is straightforward: as sample size increases, the sample mean distribution approximates a normal distribution. This holds true regardless of the population’s underlying distribution. The theorem is critical because it justifies using normal distribution assumptions in statistical analysis.
The CLT applies to sample means, not individual data points. It’s about the average of samples, not the population itself. This distinction is key to understanding CLT’s role in statistics.
The theorem works through these essential principles:
- Sample means cluster around the true population mean
- Larger sample sizes produce more accurate approximations
- The sampling distribution becomes increasingly normal as sample size grows
- Standard deviation decreases as sample size increases
Why is the Central Limit Theorem Important?
The Central Limit Theorem is important in statistics because it simplifies data analysis. It allows researchers to use normal distribution tools, even for non-normal populations. This is crucial for hypothesis testing, confidence intervals, and predictions. Without CLT, analyzing complex or skewed data would be challenging.
For instance, businesses use CLT to estimate customer behavior. They take samples of customer data, calculate averages, and predict trends. The theorem ensures these averages are reliable, even if the raw data isn’t normally distributed.
Moreover, CLT supports sample size calculations. It helps determine how large a sample needs to be for accurate results. This saves time and resources in research.
Central Limit Theorem Conditions
To apply the Central Limit Theorem, certain conditions must be met:
- Random Sampling: Samples must be randomly selected to avoid bias.
- Independence: Each sample must be independent of others.
- Sample Size: The sample size should be sufficiently large, often n ≥ 30.
However, the population shape matters. If the population is highly skewed, a larger sample size may be needed. For moderately skewed populations, n ≥ 30 is usually sufficient. For normal populations, CLT applies even with smaller samples.
These conditions ensure the sample mean distribution approximates a normal distribution. Violating them can lead to inaccurate conclusions.
Central Limit Theorem Formula
The Central Limit Theorem formula describes the sample mean distribution. It involves the population mean, standard deviation, and sample size. Here’s the formula:
Sample Mean Distribution:
μₓ̄ = μ (The sample mean equals the population mean).
σₓ̄ = σ / √n (The standard deviation of the sample mean, called standard error).
Where:
- μₓ̄ is the mean of the sample means.
- μ is the population mean.
- σₓ̄ is the standard error.
- σ is the population standard deviation.
- n is the sample size.
This formula shows that as sample size (n) increases, the standard error decreases. Smaller standard errors mean more precise estimates of the population mean.
Central Limit Theorem Examples
Let’s explore some practical Central Limit Theorem examples to clarify its application.
Example 1: Customer Spending in a Store
Suppose a store wants to estimate average customer spending. The population spending is skewed, with some customers spending much more. The store takes 50 random samples of 40 customers each. According to the Central Limit Theorem, the distribution of these sample means will be approximately normal. The store can then calculate the average of these means to estimate the population mean accurately.
Example 2: Exam Scores
A school analyzes student exam scores, which are not normally distributed. They take multiple samples of 35 students each. The CLT ensures that the distribution of sample means is normal. This allows the school to estimate the average score with confidence intervals.
These examples show how CLT applies to real-world scenarios. It makes complex data manageable and predictable.
Also Read: What is Control Limit?
Central Limit Theorem Conditions and Requirements
Essential Prerequisites for CLT Application
Central limit theorem conditions must be met for proper application. These requirements ensure the theorem works effectively across different scenarios.
Primary Conditions:
- Random sampling from the target population
- Independence between individual observations
- Adequate sample size (typically n ≥ 30)
- Finite population variance
Sample Size Considerations
What is considered a large sample size depends on population characteristics. Generally, statisticians use n = 30 as the minimum threshold. However, some distributions require larger samples for normal approximation.
The “n 30” rule provides a practical guideline for most applications. Nevertheless, symmetric populations may work with smaller samples, while skewed distributions need larger ones.
Central Limit Theorem in Statistics
In statistics, the Central Limit Theorem underpins many methods. It’s used in:
- Hypothesis Testing: CLT allows researchers to assume normality for sample means.
- Confidence Intervals: It helps calculate ranges where the population mean likely lies.
- Sample Size Calculation: CLT guides determining appropriate sample sizes.
For instance, in CLT statistics, the theorem justifies using z-scores or t-tests. These tools rely on the normal distribution of sample means. Without CLT, such methods would be less reliable.
Additionally, the theorem explains why n ≥ 30 is often considered a large sample size. It’s a rule of thumb ensuring the sample mean distribution is normal.
Common Misconceptions About CLT
Some misunderstand the Central Limit Theorem. Let’s clarify a few points:
- CLT Doesn’t Require a Normal Population: The population can be skewed or uniform. CLT still applies as sample size grows.
- CLT Applies to Sample Means, Not Individual Data: It describes the distribution of averages, not raw data.
- Sample Size Matters: Small samples (n < 30) may not yield a normal distribution if the population is highly skewed.
Understanding these points prevents misapplication of the theorem.
How to Apply the Central Limit Theorem?
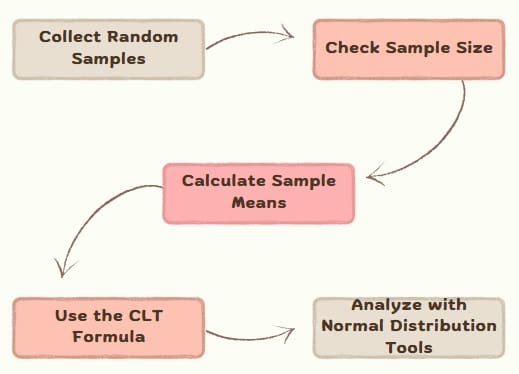
Applying the Central Limit Theorem involves a few steps:
- Collect Random Samples: Ensure samples are randomly selected and independent.
- Check Sample Size: Use n ≥ 30 for most populations. For skewed data, consider larger samples.
- Calculate Sample Means: Compute the average for each sample.
- Use the CLT Formula: Apply the formula to estimate the population mean and standard error.
- Analyze with Normal Distribution Tools: Use z-scores, t-tests, or confidence intervals for analysis.
By following these steps, researchers can make reliable inferences about populations.
Central Limit Theorem and Sample Size
Sample size is critical in CLT. A common question is, “What is a sample size?” In statistics, it’s the number of observations in a sample, denoted as “n.” The Central Limit Theorem sample size rule suggests n ≥ 30 for most cases. This ensures the sample mean distribution is approximately normal.
For highly skewed populations, larger samples (e.g., n ≥ 50) may be needed. The larger the sample, the closer the sample mean distribution is to normal. This reduces variability and improves accuracy.
Central Limit Theorem and Standard Deviation
The Central Limit Theorem also addresses standard deviation. The standard error (σₓ̄) measures the variability of sample means. It’s calculated as σ / √n. As sample size increases, the standard error decreases. This means larger samples produce more precise estimates of the population mean.
For example, if the population standard deviation is 10 and the sample size is 25, the standard error is 10 / √25 = 2. If the sample size increases to 100, the standard error drops to 10 / √100 = 1. This shows how CLT improves precision.
Also Read: What is Specification Limit?
Real-World Applications of CLT
The Central Limit Theorem has wide-ranging applications:
- Medical Research: Researchers use CLT to analyze patient data, like blood pressure averages.
- Quality Control: Manufacturers sample products to ensure quality, relying on CLT for accuracy.
- Elections: Pollsters estimate voter preferences using sample means, guided by CLT.
- Finance: Analysts predict stock returns using sample averages, assuming normality via CLT.
These applications highlight CLT’s versatility in data-driven fields.
Frequently Asked Questions (FAQs) on Central Limit Theorem
What is the Central Limit Theorem in simple terms?
The Central Limit Theorem states that sample means from any population will form a normal distribution when sample size is sufficiently large, regardless of the original population’s shape.
What does CLT mean in statistics?
CLT stands for Central Limit Theorem, a fundamental statistical concept that explains how sampling distributions behave and enables inferential statistics methods.
What sample size is needed for CLT to work?
Generally, a sample size of 30 or larger is recommended, though this can vary depending on the population distribution’s characteristics.
Does the population need to be normal for CLT?
No, the Central Limit Theorem works with any population distribution shape. The sample means will approach normality regardless of the original population’s distribution.
What is the CLT formula?
The CLT formula shows that sample means have a mean equal to the population mean (μ) and standard deviation equal to σ/√n, where σ is population standard deviation and n is sample size.



















